题目内容
7.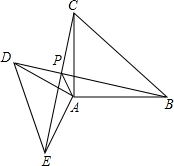 如图,在△ABC和△ADE中,∠CAB=∠DAE=90°,AB=AC=4,AD=AE=2,直线,CE交BD于点P,将△ADE绕点A旋转α角(0°<α<180°),在旋转过程中,S△PAB的最大值为2+2$\sqrt{3}$.
如图,在△ABC和△ADE中,∠CAB=∠DAE=90°,AB=AC=4,AD=AE=2,直线,CE交BD于点P,将△ADE绕点A旋转α角(0°<α<180°),在旋转过程中,S△PAB的最大值为2+2$\sqrt{3}$.
分析 根据等腰直角三角形的性质得到∠BAC=∠DAE=90°,求得∠BAD=∠CAE,根据全等三角形的性质得到∠ABD=∠ACE,推出A,B,C,P是以BC为直径的圆的点,当直线BP与⊙A(D的运动路径)相切时,直线在⊙O中截得的弦最长并且点A到直线BP的距离最大,由D在⊙A上,得到直线BD与⊙A只能相交或相切,于是得到A到BD的距离最大为⊙A的直径AD′=2,根据勾股定理得到BD′=$\sqrt{A{B}^{2}-AD{′}^{2}}$=2$\sqrt{3}$,根据三角形的面积公式即可得到结论.
解答 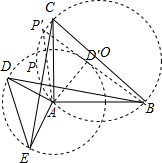 解:∵∠BAC=∠DAE=90°,
解:∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE,
∴∠ABD=∠ACE,
∴A,B,C,P是以BC为直径的圆的点,
当直线BP与⊙A(D的运动路径)相切时,直线在⊙O中截得的弦最长并且点A到直线BP的距离最大,
∵D在⊙A上,
∴直线BD与⊙A只能相交或相切,
∴A到BD的距离最大为⊙A的直径AD′=2,
∵∠AP′B=∠ACB=45°,
∴D′P′=AD′=2,
∴BD′=$\sqrt{A{B}^{2}-AD{′}^{2}}$=2$\sqrt{3}$,
∴S△PAB=$\frac{1}{2}$BP′•AD′=$\frac{1}{2}$×(2+2$\sqrt{3}$)×2=2+2$\sqrt{3}$.
故答案为:2+2$\sqrt{3}$.
点评 本题考查了旋转的性质,等腰直角三角形的性质,四点共圆,最值问题,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
19.估计二次根式$\sqrt{3}$在整数( )
| A. | 0与1之间 | B. | 1与2之间 | C. | 2与3之间 | D. | 3与4之间 |
16.若$\sqrt{1-2x}$有意义,则x的取值范围( )
| A. | x>2 | B. | x≤$\frac{1}{2}$ | C. | x≠$\frac{1}{2}$ | D. | x≤2 |
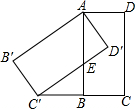 如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E.
如图,将矩形ABCD绕点A顺时针旋转,得到矩形AB′C′D′,点C的对应点C′恰好落在CB的延长线上,边AB交边C′D′于点E.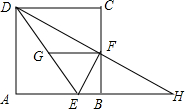 如图,正方形ABCD中,点E在AB上,且BE=$\frac{1}{4}$AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论:
如图,正方形ABCD中,点E在AB上,且BE=$\frac{1}{4}$AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论: 已知:线段a,h.
已知:线段a,h. 如图,⊙O的半径为6,AB是⊙O的弦,将线段BA绕点A逆时针旋转90°得到线段CA,当点A固定,点B在圆上运动时,则线段OC长度的最小值为6$\sqrt{2}$-6.
如图,⊙O的半径为6,AB是⊙O的弦,将线段BA绕点A逆时针旋转90°得到线段CA,当点A固定,点B在圆上运动时,则线段OC长度的最小值为6$\sqrt{2}$-6.