题目内容
17.一组割草人要把两块草地上的草割掉,大草地的面积为S,小草地的面积为$\frac{1}{2}$S,上午,全体组员都在大草地上割草,下午,一半人继续在大草地割草,到下午5时将剩下的草割完;另一半人到小草地上割草,等到下午5时还剩下一部分没割完.若上、下午的劳动时间相同,每个割草人的工作效率也相等,则没割完的这部分草地的面积是( )| A. | $\frac{1}{9}$S | B. | $\frac{1}{6}$S | C. | $\frac{1}{4}$S | D. | $\frac{1}{3}$S |
分析 设一半人半天的割草量为1份,则全体组员半天在大草地上的割草量为2份;所以在大草地上的割草量为1+2=3份.因为大草地的面积比小草地大1倍,因此小草地上的总割草量为1.5份.在这1.5份中有一半人半天割草量1份,则剩下没割完的这部分草地的面积就是0.5份,即得出结论..
解答 解:以半组人割半天为1份来看,大的一块地正好分3份割完,即S=3份,
则小草地上的总割草量为3÷2=1.5(份),
∵一半人半天割1份,
∴剩下:1.5-1=0.5(份),
∵1份=$\frac{1}{3}$S,
∴0.5份=$\frac{1}{6}$S,
故选B.
点评 本题考查了列代数式;这种类型的题目,分析起来较复杂,关键是抓住题中给出的量,得出没割完的这部分草地面积所占的份数.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
12.下列图形中,既是轴对称图形又对称轴的数量大于2条的是( )
| A. |  | B. |  | C. |  | D. |  |
2.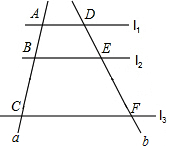 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$等于( )
如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$等于( )
 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$等于( )
如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$等于( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
9.下列等式从左到右的变形,属于因式分解的是( )
| A. | a(x-y)=ax-ay | B. | x2-9=(x+3)(x-3) | C. | (x+1)(x+2)=x2+3x+2 | D. | x2+2x+1=x(x+2)+1 |
6. 如图,△ABC≌△DCB,若AC=13,DE=4,则BE的长为( )
如图,△ABC≌△DCB,若AC=13,DE=4,则BE的长为( )
 如图,△ABC≌△DCB,若AC=13,DE=4,则BE的长为( )
如图,△ABC≌△DCB,若AC=13,DE=4,则BE的长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
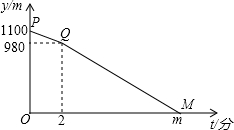 已知A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象解答:
已知A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象解答: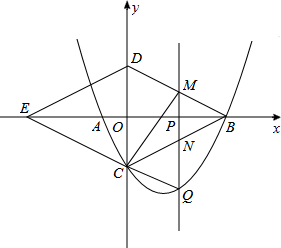 如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$ x-4与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$ x-4与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.