题目内容
8.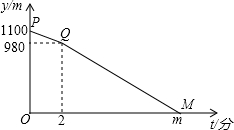 已知A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象解答:
已知A,B两地相距1100米,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2分钟,乙出发7分钟后与甲相遇.设甲、乙两人相距y米,甲行进的时间为t分钟,y与t之间的函数关系如图所示.请你结合图象解答:(1)求甲的行进速度和点M的坐标;
(2)求直线PQ对应的函数表达式;
(3)求乙的行进速度.
分析 (1)根据速度=路程÷时间即可算出甲的行进速度,再用甲先出发的时间加速二者相遇时乙出发的时间即可得出点M的横坐标,从而得出点M的坐标;
(2)设直线PQ对应的函数表达式为y=kx+b(k≠0),根据点的坐标利用待定系数法即可求出直线PQ对应的函数表达式;
(3)根据乙的行进速度=路程÷时间-甲的行进速度,代入数据即可得出结论.
解答 解:(1)甲的行进速度为(1100-980)÷2=60(米/分钟),
点M的横坐标为2+7=9,
∴点M的坐标为(9,0).
(2)设直线PQ对应的函数表达式为y=kx+b(k≠0),
将(0,1100)、(2,980)代入y=kx+b,
$\left\{\begin{array}{l}{b=1100}\\{2k+b=980}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-60}\\{b=1100}\end{array}\right.$,
∴直线PQ对应的函数表达式为y=-60x+1100.
(3)乙的行进速度为980÷7-60=80(米/分钟).
答:乙的行进速度为80米/分钟.
点评 本题考查了一次函数的应用以及待定系数法求函数解析式,根据点的坐标利用待定系数法求出函数表达式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.在下列各组条件中,不能判定△ABC与△DEF全等的是( )
| A. | AB=DE,∠B=∠E,∠C=∠F | B. | AC=DF,BC=EF,∠C=∠F | ||
| C. | AB=DE,BC=EF,∠A=∠D | D. | ∠A=∠D,∠C=∠F,AC=DF |
16.下列长度的三条线段,能组成三角形的是( )
| A. | 3,4,8 | B. | 5,6,11 | C. | 6,8,16 | D. | 5,6,10 |
3.若∠α与∠β互为补角,∠β是∠α的2倍,则∠α为( )
| A. | 30° | B. | 40° | C. | 60° | D. | 120° |
20.小华想了解贵阳市的气温情况,他把所调查的7天的气温制作了如下表格:
对这7天气温情况,去掉一个最高温度和一个最低温度,表格中的统计量一定不发生变化的是中位数.
| 平均数 | 中位数 | 众数 | 方差 |
| 20.9℃ | 21.5℃ | 22℃ | 8.3 |
17.一组割草人要把两块草地上的草割掉,大草地的面积为S,小草地的面积为$\frac{1}{2}$S,上午,全体组员都在大草地上割草,下午,一半人继续在大草地割草,到下午5时将剩下的草割完;另一半人到小草地上割草,等到下午5时还剩下一部分没割完.若上、下午的劳动时间相同,每个割草人的工作效率也相等,则没割完的这部分草地的面积是( )
| A. | $\frac{1}{9}$S | B. | $\frac{1}{6}$S | C. | $\frac{1}{4}$S | D. | $\frac{1}{3}$S |
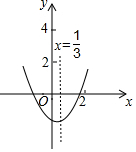 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②abc>0,③a-b+c>0,④2a-3b=0,⑤c-4b>0.其中正确结论的个数有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②abc>0,③a-b+c>0,④2a-3b=0,⑤c-4b>0.其中正确结论的个数有( )