题目内容
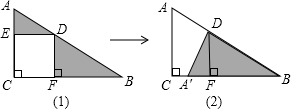如图△ABC中有正方形EDFC，由图（1）通过三角形的旋转变换可以得到图（2）．观察图形的变换方式，若AD=3，DB=4，则图（1）中△ADE和△BDF面积之和S为考点：旋转的性质
专题：
分析：由图形可知△DA′F是由△DAE旋转得到，利用旋转的性质可得到△A′DB为直角三角形，可求得S，在Rt△A′DB中 由勾股定理可求得A′B，再利用面积相等可求得DF，可求得正方形EDFC的面积．
解答：解：由旋转的性质得AD=A′D=3，∠ADE=∠A′DF，
∵∠A′DB=∠A′DF+∠FDB=∠ADE+∠FDB=90°，
∴在Rt△A′DB中，
S△A′DB=
A′D×BD=
×3×4=6，
∴S△ADE+S△BDF=S△A′DF+S△BDF=S△A′DB=6，
又A′D=3，BD=4，可求得A′B=5，
∴
A′B•DF=
×5×DF=6，
∴DF=
，
∴S正方形EDFC=DF2=
，
故答案为：6；
．
∵∠A′DB=∠A′DF+∠FDB=∠ADE+∠FDB=90°，
∴在Rt△A′DB中，
S△A′DB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ADE+S△BDF=S△A′DF+S△BDF=S△A′DB=6，
又A′D=3，BD=4，可求得A′B=5，
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴DF=
| 12 |
| 5 |
∴S正方形EDFC=DF2=
| 144 |
| 25 |
故答案为：6；
| 144 |
| 25 |
点评：本题主要考查旋转的性质，利用旋转得到△A′DB为直角三角形是解题的关键，注意勾股定理及等积法的应用．
练习册系列答案
阅读快车系列答案
相关题目
AB=CD，AE⊥BC于E，DF⊥BC于F，且CE=BF．求证：
从△ABC的顶点A引三条线段：∠A的平分线AM，∠A的外角平分线AN，三角形外接圆的切线AK，点M、K、N依次排列在直线BC上，证明：MK=KN．已知世运会、亚运会、奥运会分别于2009年、2010年、2012年举办，若这三项运动会均每四年举办一次，则这三项运动会都不举办的那一年是（ ）
| A、2063年 |
| B、2064年 |
| C、2065年 |
| D、2066年 |
如图，从C到B地有①②③条路线可以走，每条路线长分别为l，m，n （ ）| A、l＞m＞n |
| B、l=m＞n |
| C、m＜n=l |
| D、l＞n＞m |