题目内容
19.(1)($\sqrt{2}$+$\sqrt{3}$)($\sqrt{2}$-$\sqrt{3}$)+(2$\sqrt{2}$+3$\sqrt{3}$)2(2)已知x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,求x2+xy+y2值.
分析 (1)利用平方差公式和完全平方公式展开后合并即可得;
(2)将x、y的值代入原式=(x+y)2-xy,利用平方差公式和完全平方公式计算可得.
解答 解:(1)原式=2-3+8+12$\sqrt{6}$+27=34+12$\sqrt{6}$;
(2)当x=$\sqrt{3}$+1,y=$\sqrt{3}$-1时,
原式=(x+y)2-xy.
=($\sqrt{3}$+1+$\sqrt{3}$-1)2-($\sqrt{3}$+1)($\sqrt{3}$-1)
=12-(3-1)
=10.
点评 本题主要考查二次根式的化简求值和完全平方公式及平方差公式的运用,熟练掌握平方差公式和完全平方公式的变形及二次根式的性质是解题的关键.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
10.将抛物线y=$\frac{1}{2}$x2向左平移一个单位,所得抛物线的解析式为( )
| A. | y=$\frac{1}{2}$x2+1 | B. | y=$\frac{1}{2}$x2-1 | C. | y=$\frac{1}{2}$(x+1)2 | D. | y=$\frac{1}{2}$(x-1)2 |
4.下列问题中,两个变量成反比例函数的是( )
| A. | 矩形面积固定,长x和宽y的关系 | B. | 矩形周长固定,长x和宽y的关系 | ||
| C. | 正方形面积S和边长a之间的关系 | D. | 正方形周长C和边长a之间的关系 |
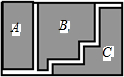 如图,为方便行人,需在长方形的草坪中修建宽都为1m的小路,将草坪划分为A,B,C三个区域,已知原长方形的长为77m,宽为41m,其余部分种植草坪,则草坪的面积为3000平方米.
如图,为方便行人,需在长方形的草坪中修建宽都为1m的小路,将草坪划分为A,B,C三个区域,已知原长方形的长为77m,宽为41m,其余部分种植草坪,则草坪的面积为3000平方米.