题目内容
11．设m=$\frac{ab}{{a}^{2}-ab}$，则$\frac{{m}^{2}}{am-b}$-$\frac{m}{a}$可化简为$\frac{1}{a}$．分析 把$\frac{{m}^{2}}{am-b}$-$\frac{m}{a}$化简，代入m=$\frac{ab}{{a}^{2}-ab}$=$\frac{b}{a-b}$即可得到结论．
解答 解：∵$\frac{{m}^{2}}{am-b}$-$\frac{m}{a}$=m（$\frac{m}{am-b}$-$\frac{1}{a}$），
∵m=$\frac{ab}{{a}^{2}-ab}$=$\frac{b}{a-b}$，
∴$\frac{b}{a-b}$•（$\frac{\frac{b}{a-b}}{\frac{ab}{a-b}-b}$-$\frac{1}{a}$）=$\frac{b}{a-b}$•$\frac{a-b}{ab}$=$\frac{1}{a}$，
故答案为：$\frac{1}{a}$．
点评 本题考查了分式的化简求值，难度适中，关键是先把原分式化为最简，再利用已知条件求解．
练习册系列答案
相关题目
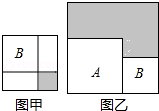有两个正方形A，B，现将B放在A的内部得图甲，将A，B并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为2和13，则正方形A，B的面积之和为15．
小明发现：作两条互相垂直的直线MN、PQ，垂足为O，作∠PON的角平分线OE，点A、B分别是OE、PQ上任意一点，再作∠ABP的平分线BD，BD的反向延长线交∠OAB的平分线于点C，∠C的大小是不随A、B的变化而变化的，是一个定值，∠C为22.5°．