题目内容
已知关于x的一元二次方程mx2-(3m-2)x+2m-2=0有两个不相等的实数根,则m的取值范围为 .
考点:根的判别式,一元二次方程的定义
专题:
分析:由二次项系数不为0,且根的判别式大于0,求出m的范围即可.
解答:解:∵关于x的一元二次方程mx2-(3m-2)x+2m-2=0有两个不相等的实数根,
∴m≠0且△=(3m-2)2-4m(2m-2)=(m-2)2>0,
则m的范围为m≠0且m≠2.
故答案为:m≠0且m≠2.
∴m≠0且△=(3m-2)2-4m(2m-2)=(m-2)2>0,
则m的范围为m≠0且m≠2.
故答案为:m≠0且m≠2.
点评:此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、若|a|=a,则a=0 |
| B、两点之间,直线最短 |
| C、直线AB和直线BA是同一条直线 |
| D、多项式x3+x2的次数是5 |
 如图,AB为⊙O的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )
如图,AB为⊙O的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )| A、5 | ||
| B、8 | ||
C、2
| ||
D、4
|
 如图,无法保证△ADE与△ABC相似的条件是( )
如图,无法保证△ADE与△ABC相似的条件是( )| A、∠1=∠C | ||||
| B、∠A=∠C | ||||
| C、∠2=∠B | ||||
D、
|
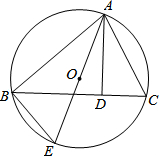 如图,AE是△ABC外接圆O的直径,连结BE,作AD⊥BC于D.
如图,AE是△ABC外接圆O的直径,连结BE,作AD⊥BC于D.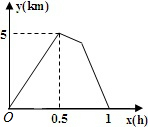 甲、乙二人同时从A地到B地,甲骑自行车,乙步行,甲到B地后休息了十分钟然后以相同的速度返回,在返回途中与乙相遇,甲、乙二人之间的距离y(km)与乙步行时间x(h)之间的关系如图,则甲从出发到返回与乙相遇共走了
甲、乙二人同时从A地到B地,甲骑自行车,乙步行,甲到B地后休息了十分钟然后以相同的速度返回,在返回途中与乙相遇,甲、乙二人之间的距离y(km)与乙步行时间x(h)之间的关系如图,则甲从出发到返回与乙相遇共走了