题目内容
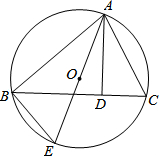如图，AE是△ABC外接圆O的直径，连结BE，作AD⊥BC于D．（1）求证：△ABE∽△ADC；
（2）若AB=8，AC=6，AE=10，求AD的长．
考点：相似三角形的判定与性质,圆周角定理
专题：
分析：（1）如图，证明∠ABE=∠ADC=90°，∠E=∠C，即可解决问题．
（2）由△ABE∽△ADC，列出比例式
=
，求出AD即可解决问题．
（2）由△ABE∽△ADC，列出比例式
| AB |
| AD |
| AE |
| AC |
解答： 解：（1）如图，∵AE是△ABC外接圆O的直径，且AD⊥BC，
∴∠ABE=∠ADC=90°；而∠E=∠C，
∴△ABE∽△ADC．
（2）∵△ABE∽△ADC，
∴
=
，而AB=8，AC=6，AE=10，
∴AD=4.8．
解：（1）如图，∵AE是△ABC外接圆O的直径，且AD⊥BC，∴∠ABE=∠ADC=90°；而∠E=∠C，
∴△ABE∽△ADC．
（2）∵△ABE∽△ADC，
∴
| AB |
| AD |
| AE |
| AC |
∴AD=4.8．
点评：该题主要考查了相似三角形的判定及其性质、圆周角定理及其推论等几何知识点及其应用问题；解题的关键是深入观察图形结构特点，数形结合，准确找出图形中隐含的相等或相似关系．
练习册系列答案
53天天练系列答案
相关题目
若△ABC∽△A′B′C′，则相似比k等于（ ）
| A、A′B′：AB |
| B、∠A：∠A' |
| C、S△ABC：S△A′B′C′ |
| D、△ABC周长：△A′B′C′周长 |
如图，⊙O的直径AB⊥弦CD，且∠BAC=40°，则∠BOD的度数为（ ）| A、20° | B、30° |
| C、40° | D、80° |
为了估计鱼塘中鱼的条数，养鱼者首先从鱼塘中捕获n条鱼，在每一条鱼身上做好记号后把这些鱼放归鱼塘．再从鱼塘中捞a条鱼，如果在这a条鱼中有b条鱼是有记号的，那么估计鱼塘中鱼的条数大约为（ ）
| A、bn | ||
| B、an | ||
C、
| ||
D、
|
在平面直角坐标系上，点（4，6）先向左平移6个单位，再将得到的点的坐标关于x轴对称，得到的点位于（ ）
| A、x轴上 | B、y轴上 |
| C、第三象限 | D、第四象限 |
反比例函数y=
经过点（-1，2），则2014a的值是（ ）
| a-2 |
| x |
| A、2009 | B、0 | C、1 | D、-1 |