题目内容
11.在探究“抛物线y=x2-2x-3与x轴交于A、B两点(A在B的左边),过点A且与x轴成45°角的直线,与抛物线交于点C”的图形性质时,小慧在得出“在第一象限存在一点C1,第四象限存在一点C2满足条件”这一正确结论后,还由此得出下列结论:①C1的横坐标为4,C2的纵坐标为-3;②sin∠AC1C2=$\frac{{3\sqrt{34}}}{34}$;③过点C1、C2作x轴的垂线,垂足分别为D1、D2,则△C1D1B∽△C2D2B,则其中正确的为( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
分析 利用方程组求出C1,C2的坐标,即可一一判断.
解答 解:由题意A(-1,0),B(3,0),
由$\left\{\begin{array}{l}{y=x+1}\\{y={x}^{2}-2x-3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$,
∵A(-1,0),
∴C1(4,5),
由$\left\{\begin{array}{l}{y=-x-1}\\{y={x}^{2}-2x-3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$,
∴C2(2,-3),故①正确,
∴AC2=3$\sqrt{2}$,C1C2=2$\sqrt{17}$,
∴sin∠AC1C2=$\frac{A{C}_{2}}{{C}_{1}{C}_{2}}$=$\frac{3\sqrt{2}}{2\sqrt{17}}$=$\frac{3\sqrt{34}}{34}$,故②正确,
∵$\frac{{C}_{1}{D}_{1}}{B{D}_{1}}$≠$\frac{{C}_{2}{D}_{2}}{B{D}_{2}}$,故③错误,
故选A.
点评 本题考查相似三角形的判定、抛物线与x轴的交点、解直角三角形等知识,解题的关键是学会利用方程组求两个函数图象的交点坐标,属于中考常考题型.

| A. | m6÷m2=m3 | B. | (x+1)2=x2+1 | C. | (3m2)3=9m6 | D. | 2a3•a4=2a7 |
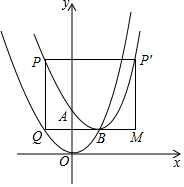 如图,在平面直角坐标系中,抛物线y=a(x-2)2+2经过点A(0,4),与其对称轴交于点B,P为抛物线y=a(x-2)2+2上一点,过点P分别作x轴、y轴的垂线,交抛物线y=a(x-h)2+h于点Q,交抛物线y=a(x-2)2+2于点P′,以PQ、PP′为邻边作矩形PP′MQ,设点P的横坐标为m(m≤0).
如图,在平面直角坐标系中,抛物线y=a(x-2)2+2经过点A(0,4),与其对称轴交于点B,P为抛物线y=a(x-2)2+2上一点,过点P分别作x轴、y轴的垂线,交抛物线y=a(x-h)2+h于点Q,交抛物线y=a(x-2)2+2于点P′,以PQ、PP′为邻边作矩形PP′MQ,设点P的横坐标为m(m≤0).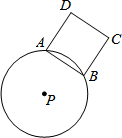 如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为( )
如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为( )