题目内容
4.一个不透明的口袋里有4个除颜色外都相同的球,其中有3个红球,1个黄球.(1)若从中随意摸出两个球,用树状图或列表法求摸出两个红球的概率;
(2)若要使从中随意摸出一个球是黄球的概率为$\frac{2}{3}$,求袋子中需再加入几个黄球?
分析 (1)求出摸到红球的概率即可;
(2)设需再加入x个黄球,根据摸出黄球的概率为$\frac{2}{3}$列出方程求解即可.
解答  解:(1)∵从中随意摸出两个球的所有可能的结果个数是12,
解:(1)∵从中随意摸出两个球的所有可能的结果个数是12,
随意摸出两个球是红球的结果个数是6,
∴从中随意摸出两个球的概率=$\frac{6}{12}$=$\frac{1}{2}$;
(2)设需再加入x个黄球.
依题意可列:$\frac{1+x}{3+1+x}$=$\frac{2}{3}$,
解得x=5
∴要使从中随意摸出一个球是黄球的概率为$\frac{2}{3}$,袋子中需再加入5个黄球.
点评 考查了可能性的大小,对于这类题目,可算出球的总个数,要求某种球被摸到的可能性,就看这种球占总数的几分之几就可以了.

练习册系列答案
相关题目
16.2014年杭州市普高招生报考人数共约49500人,将49500用科学记数法表示为( )
| A. | 495×102 | B. | 49.5×103 | C. | 4.95×104 | D. | 0.495×105 |
13.若a>b,则下列式子正确的是( )
| A. | a-4>b-3 | B. | $\frac{1}{2}$a<$\frac{1}{2}b$ | C. | 2a+3>2b+3 | D. | -3a>-3b |
14.点M在第二象限,它到x轴、y轴的距离分别为4和2,则点M的坐标为( )
| A. | (4,2) | B. | (-2,4) | C. | (-4,-2) | D. | (2,4) |
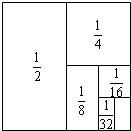 如图:把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的正方形,接着把其中一个面积为$\frac{1}{2}$的正方形等分成两个面积为$\frac{1}{4}$的正方形,再把其中一个面积为$\frac{1}{4}$的正方形等分成两个面积为$\frac{1}{8}$的正方形,如此进行下去,试观察图形来计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{256}$.
如图:把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的正方形,接着把其中一个面积为$\frac{1}{2}$的正方形等分成两个面积为$\frac{1}{4}$的正方形,再把其中一个面积为$\frac{1}{4}$的正方形等分成两个面积为$\frac{1}{8}$的正方形,如此进行下去,试观察图形来计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{256}$.