题目内容
3.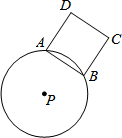 如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为( )
如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为( )| A. | 3π | B. | 6π | C. | 9π | D. | 12π |
分析 连接PD,过点P作PE⊥CD与点E,PE交AB于点F,则CD边扫过的面积为以PD为外圆半径、PE为内圆半径的圆环面积,利用垂径定理即可得出AF=BF,进而可得出DE=CE=3,再根据圆环的面积公式结合勾股定理即可得出CD边扫过的面积.
解答 解:连接PD,过点P作PE⊥CD与点E,PE交AB于点F,则CD边扫过的面积为以PD为外圆半径、PE为内圆半径的圆环面积,如图所示.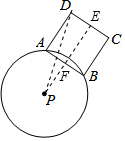
∵PE⊥CD,AB∥CD,
∴PF⊥AB.
又∵AB为⊙P的弦,
∴AF=BF,
∴DE=CE=$\frac{1}{2}$CD=$\frac{1}{2}$AB=3,
∴CD边扫过的面积为π(PD2-PE2)=π•DE2=9π.
故选C.
点评 本题考查了垂径定理、勾股定理、平行线的性质以及圆环的面积公式,结合AB边的旋转,找出CD边旋转过程中扫过区域的形状是关键.

练习册系列答案
相关题目
8.如图所示的整式化简过程,对于所列的每一步运算,依据错误的是( )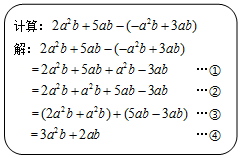
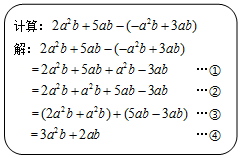
| A. | ①:去括号法则 | B. | ②:加法交换律 | ||
| C. | ③:等式的基本性质 | D. | ④:合并同类项法则 |
16.2014年杭州市普高招生报考人数共约49500人,将49500用科学记数法表示为( )
| A. | 495×102 | B. | 49.5×103 | C. | 4.95×104 | D. | 0.495×105 |
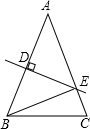 如图,在△ABC中,AB=AC,AB的中垂线DE交AC于E,△BCE的周长为15,BC=7,则AB的长为8.
如图,在△ABC中,AB=AC,AB的中垂线DE交AC于E,△BCE的周长为15,BC=7,则AB的长为8.