Question

5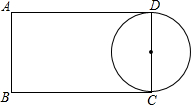．如图，矩形ABCD中，AB=4，AD=7，点E，F分别在边AD、BC上，且B、F关于过点E的直线对称，如果以CD为直径的圆与EF相切，那么AE=3．

Answer 1

分析 设⊙O与EF相切于M，连接EB，作EH⊥BC于H．由题意易知四边形AEHB是矩形，设AE=BH=x，由切线长定理可知，ED=EM，FC=FM，由B、F关于EH对称，推出HF=BH=x，ED=EM=7-x，FC=FM=7-2x，EF=14-3x，在Rt△EFH中，根据EF²=EH²+HF²，列出方程即可解决问题．

解答 解：如图，设⊙O与EF相切于M，连接EB，作EH⊥BC于H．

由题意易知四边形AEHB是矩形，设AE=BH=x，
由切线长定理可知，ED=EM，FC=FM，
∵B、F关于EH对称，
∴HF=BH=x，ED=EM=7-x，FC=FM=7-2x，EF=14-3x，
在Rt△EFH中，∵EF²=EH²+HF²，
∴4²+x²=（14-3x）²，
解得x=3或$\frac{15}{2}$（舍弃），
∴AE=3，
故答案为3．

点评 本题考查切线的性质、矩形的性质、轴对称的性质、勾股定理等知识，解题的关键是灵活运用所学知识解决问题，学会用方程的思想思考问题，属于中考常考题型．