题目内容
15.关于x的二次函数y1=kx2+(2k-1)x-2(k为常数)和一次函数y2=x+2.(1)若k=2,求函数y1的顶点坐标;
(2)若函数y1的图象不经过第一象限,求k的取值范围;
(3)已知函数y1的图象与x轴的两个交点间的距离等于3,
①试求此时k的值;
②若y1>y2,试求x的取值范围.
分析 (1)将k=2时的函数解析式配方成顶点式即可得;
(2)由该抛物线与x轴的交点为(-2,0)、($\frac{1}{k}$,0),与y轴的交点为(0,-2),根据函数y1的图象不经过第一象限知点($\frac{1}{k}$,0)必不在x轴的正半轴上,据此解答即可;
(3)①根据两点间的距离公式列出关于k的方程求解可得;
②分k=1和k=-$\frac{1}{5}$两种情况,依据y1>y2列出关于x的不等式,解之可得.
解答 解:(1)当k=2时,y1=2x2+3x-2=2(x+$\frac{3}{4}$)2-$\frac{25}{8}$,
∴顶点坐标为(-$\frac{3}{4}$,-$\frac{25}{8}$);
(2)∵y1=2(x+2)(x-$\frac{1}{k}$),
∴该抛物线与x轴的交点为(-2,0)、($\frac{1}{k}$,0),与y轴的交点为(0,-2),
而函数y1的图象不经过第一象限,
∴点($\frac{1}{k}$,0)必不在x轴的正半轴上,
∴$\frac{1}{k}$<0,即k<0;
(3)①∵y1的图象与x轴的两个交点间的距离等于3,
∴$\frac{1}{k}$+2=±3,
解得:k1=1,k2=-$\frac{1}{5}$;
②当k=1时,y1=(x+2)(x-1),y2=x+2
∵y1>y2,
∴(x+2)(x-1)>x+2,即(x+2)(x-2)>0,
解得:x<-2或x>2;
当k=-$\frac{1}{5}$时,
∵y1>y2,
∴-$\frac{1}{5}$(x+2)(x+5)>x+2,即(x+2)(x+10)<0,
解得:-10<x<-2.
点评 本题主要考查二次函数与不等式组及二次函数与x轴的交点,熟练掌握二次函数的图象和性质是解题的关键.

| A. | 口袋中有8个白球,从口袋中任取一球,会摸到黑球 | |
| B. | 早上太阳从西方升起 | |
| C. | 地球围绕太阳转 | |
| D. | 一觉醒来,天气晴朗 |
| A. | 48 | B. | 40 | C. | 30 | D. | 12 |
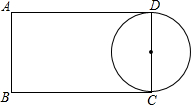 如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE=3.
如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE=3.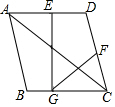 已知:如图,平行四边形ABCD中,点E,F分别是AD,CD的中点,EG⊥BC,垂足为点G,连接FG,求证:AC=2GF.
已知:如图,平行四边形ABCD中,点E,F分别是AD,CD的中点,EG⊥BC,垂足为点G,连接FG,求证:AC=2GF.
 如图,圆柱体的高为4cm,底面周长为6cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图所示,则最短路程为5cm.
如图,圆柱体的高为4cm,底面周长为6cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图所示,则最短路程为5cm.