题目内容
15.(1)解下列方程和不等式.①$\frac{x}{x-3}$+$\frac{2-x}{3-x}$=1
②$\frac{x-3}{2}$+3≥x+1
(2)分解因式:
①m2n-6mn+9n
②(x-1)(x-3)+1.
分析 (1)①分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
②不等式去分母,移项合并,把x系数化为1,即可求出解集;
(2)①原式提取公因式,再利用完全平方公式分解即可;
②原式整理后,利用完全平方公式分解即可.
解答 解:(1)①去分母得:x+x-2=x-3,
解得:x=-1,
经检验x=-1是分式方程的解;
②去分母得:x-3+6≥2x+2,
解得:x≤1;
(2)①原式=n(m2-6m+9)=n(m-3)2;
②原式=x2-4x+4=(x-2)2.
点评 此题考查了解分式方程,提公因式法与公式法的综合运用,以及解一元一次不等式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知(x1,y1)和(x2,y2)是直线y=-3x上的两点,且x1<x2,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 以上都有可能 |
 如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,已知菱形ABCD的周长为20cm,则 OE长为5cm.
如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,已知菱形ABCD的周长为20cm,则 OE长为5cm. 实数a,b在数轴上的位置如图所示,则化简$\sqrt{(a-1)^{2}}$-$\sqrt{(a-b)^{2}}$+|b-2|的结果是-1.
实数a,b在数轴上的位置如图所示,则化简$\sqrt{(a-1)^{2}}$-$\sqrt{(a-b)^{2}}$+|b-2|的结果是-1. 如图,枣庄两条公路OA和OB相交于点O,在∠AOB内部有小区C和D,现要建一个大型购物超市P,使点P到路OA、OB的距离相等,且到小区C和D的距离也相等,用尺规作出超市P的位置.(不写作法,保留作图痕迹,写出结论).
如图,枣庄两条公路OA和OB相交于点O,在∠AOB内部有小区C和D,现要建一个大型购物超市P,使点P到路OA、OB的距离相等,且到小区C和D的距离也相等,用尺规作出超市P的位置.(不写作法,保留作图痕迹,写出结论).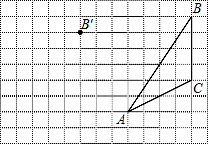 如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.
如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.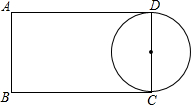 如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE=3.
如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE=3.