Question

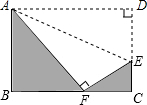如图，将矩形ABCD沿直线AE折叠，顶点D恰好落在ABC边上F点处，已知CE=4cm，AB=9cm，则矩形ABCD的面积为

 

m²．

Answer 1

考点：翻折变换（折叠问题）

专题：

分析：如图，证明EF=DE=5；求出CF=3；证明△ABF∽△FCE，列出比例式，即可解决问题．

解答：解：由题意得：AF=AD（设为λ），EF=DE，∠AFE=∠D=90°；
∵四边形ABCD是矩形，
∴CD=AB=9，∠B=∠C=90°；而CE=4，
∴EF=DE=5；由勾股定理得：CF=3；
∴BF=λ-3；
∵∠BAF+∠AFB=∠AFB+∠EFC，
∴∠BAF=∠EFC，而∠B=∠C，
∴△ABF∽△FCE，
∴

AF

EF

=

BF

CE

，即

λ

5

=

λ-3

4

，
解得：λ=15，
∴矩形ABCD的面积=15×9=135（m²）．
故答案为：135．

点评：该题主要考查了翻折变换的性质及其应用问题；解题的关键是灵活运用翻折变换的性质、勾股定理、相似三角形的判定及其性质等知识点来分析、解答．