题目内容
10．
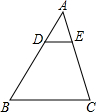如图所示，若DE∥BC，$\frac{AD}{BD}=\frac{1}{2}$，求$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$．
分析 因为DE∥BC，所以可以判断△ADE∽△ABC，根据AD：BD=1：2可以判断出两三角形的面积比，进而判断出S△ADE：S四边形DEBC的比值．
解答 解：∵AD：BD=1：2，
∴AD：AB=1：3，
∵DE∥BC，
∴△ADE∽△ABC，
∵相似三角形的相似比是1：3，
∴面积的比是1：9，
设△ADE的面积是a，则△ABC的面积是9a，则四边形DEBC的面积是8a，
∴S△ADE：S四边形DEBC=1：8．
点评 本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
智能训练练测考系列答案
相关题目
y24-2×
=607．
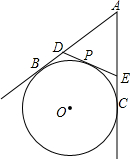已知：如图，AB，AC是⊙O的切线，B，C是切点，过$\widehat{BC}$上的任意一点P作⊙O的切线与AB，AC分别交于点D，E．
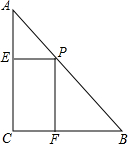已知a、b为直角三角形两直角边，且a、b为一元二次方程：x2-（2k+1）x+k2+k+$\frac{1}{4}$=0的两根．
如图，△ABC中，EF∥BC，AD交EF于G，已知EG=2，GF=3，BD=5，求DC的长．