题目内容
19．已知在△ABC中，AD⊥BC于点D，若AB=AC=2cm，AD=$\sqrt{2}$cm，求BC的长．分析 先利用等腰三角形三线合一的性质得出BC=2BD．然后在Rt△ABD中，利用勾股定理求出BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{2}$cm，于是BC=2$\sqrt{2}$cm．
解答 
解：∵AB=AC，AD⊥BC于点D，
∴BC=2BD．
∵在Rt△ABD中，∠ADB=90°，AB=2cm，AD=$\sqrt{2}$cm，
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{2}$cm，
∴BC=2$\sqrt{2}$cm．
点评 本题考查了勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．也考查了等腰三角形三线合一的性质．
练习册系列答案
相关题目
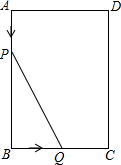如图在矩形ABCD中，AB=8cm，Bc=6cm，动点P，Q分别从A，B向B、C运动，运动速度为1cm/s，当P、Q一点停止运动则另一点停止运动．设△PBQ的面积为y，点P、Q运动时间为x（s）．
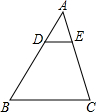如图所示，若DE∥BC，$\frac{AD}{BD}=\frac{1}{2}$，求$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$．
（1）用式子表示图中阴影部分的面积；
如图，在△ABC中，PM，PN分别为边AB，AC的垂直平分线，且它们交于点P，求证：点P也在边BC的垂直平分线上．
如图，在△ABC中，AC=4，BC=3，CD⊥AB于点D，BD=2，求tanA，tanB的值．