题目内容
17．阅读材料：求1+2+22+23+24+…+220的值．解：设S=1+2+22+23+24+…+220，将等式两边同时乘以2得：2S=2+22+23+24+25+…+221
将下式减去上式得2S-S=221-1
即S=221-1
即1+2+22+23+24+…+220=221-1
请你仿照此法计算：
（1）1+2+22+23+24+…+22016
（2）1+2+22+23+24+…+2n（其中n为正整数）
（3）1+5+52+53+54+…+5n（其中n为正整数）
分析 （1）设原式=S，两边乘以2变形得到关系式，两式相减即可求出S；
（2）设原式=S，两边乘以2变形得到关系式，两式相减即可求出S；
（3）设原式=S，两边乘以5变形得到关系式，两式相减即可求出S．
解答 解：（1）设S=1+2+22+23+24+…+22016，
两边乘以2得：2S=2+22+23+24+…+22017，
下式减去上式得：S=22017-1；
（2）设S=1+2+22+23+24+…+2n
两边乘以2得：2S=2+22+23+24+…+2n+1，
下式减去上式得：S=2n+1-1；
（3）设S=1+5+52+53+54+…+5n，
两边乘以5得：5S=5+52+53+54+…+5n+1，
下式减去上式得：4S=5n+1-1，即S=$\frac{{5}^{n+1}-1}{4}$，
则1+5+52+53+54+…+5n=$\frac{{5}^{n+1}-1}{4}$．
点评 本题考查数字的变化类，解题的关键是明确题意，找出数字的变化特点．
练习册系列答案
阅读快车系列答案
相关题目
在矩形纸片ABCD中，AB=4，BC=10，E是AD边的中点，把矩形纸片沿过点E的直线折叠，使点A落在BC边上，则折痕EF的长为$\frac{5\sqrt{5}}{2}$．
12．某县以“重点整治环境卫生”为抓手，加强对各乡镇环保建设的投入，计划从2017年起到2019年累计投入4250万元，已知2017年投入1500万元，设投入经费的年平均增长率为x，根据题意，下列所列方程正确的是（ ）
| A． | 1500（1+x）2=4250 | B． | 1500（1+2x）=4250 | ||
| C． | 1500+1500x+1500x2=4250 | D． | 1500（1+x）+1500（1+x）2=4250-1500 |
如图，△ABC中，BC=5，sinA=$\frac{3}{5}$
如图，海中有一个小岛B，它的周围14海里内有暗礁，在小岛正西方有一点A测得在北偏东60°，方向上有一灯塔C，灯塔C在小岛B北偏东15°方向上20海里处，渔船跟踪鱼群沿AC方向航行，每小时航行10$\sqrt{2}$海里．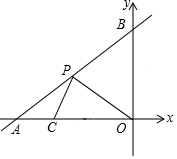
如图，直线y=x+6与x轴、y轴分别交于点A和点B，x轴上有一点C（-4，0），点P为直线一动点，当PC+PO值最小时点P的坐标为（-$\frac{9}{2}$，$\frac{3}{2}$）．