题目内容
6.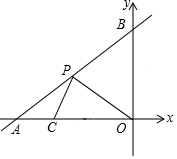 如图,直线y=x+6与x轴、y轴分别交于点A和点B,x轴上有一点C(-4,0),点P为直线一动点,当PC+PO值最小时点P的坐标为(-$\frac{9}{2}$,$\frac{3}{2}$).
如图,直线y=x+6与x轴、y轴分别交于点A和点B,x轴上有一点C(-4,0),点P为直线一动点,当PC+PO值最小时点P的坐标为(-$\frac{9}{2}$,$\frac{3}{2}$).
分析 作点C关于直线y=x+6的对称点C′,连接AC′,OC′交直线y=x+6于点P,则点P即为所求.求出AB两点的坐标,据此可得出∠BAO及∠ACC′的度数,根据轴对称的性质得出△ACC′是等腰直角三角形,故可得出C′点的坐标,利用待定系数法求出直线OC′的坐标,进而可得出P点坐标.
解答  解:如图,作点C关于直线y=x+6的对称点C′,连接AC′,
解:如图,作点C关于直线y=x+6的对称点C′,连接AC′,
OC′交直线y=x+6于点P,则点P即为所求,
∵直线y=x+6与x轴、y轴分别交于点A和点B,
∴A(-6,0),B(0,6),
∴∠BAO=45°.
∵CC′⊥AB,
∴∠ACC′=45°.
∵点C,C′关于直线AB对称,
∴AB是线段CC′的垂直平分线,
∴△ACC′是等腰直角三角形,
∴AC=AC′=2,
∴C′(-6,2).
设直线OC′的解析式为y=kx(k≠0),则2=-6k,解得k=-$\frac{1}{3}$,
∴直线OC′的解析式为y=-$\frac{1}{3}$x,
∴$\left\{\begin{array}{l}{y=-\frac{1}{3}x}\\{y=x+6}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{9}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,
∴P(-$\frac{9}{2}$,$\frac{3}{2}$).
故答案为:(-$\frac{9}{2}$,$\frac{3}{2}$).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列实数是无理数的是( )
| A. | -1 | B. | $\sqrt{3}$ | C. | 3.14 | D. | $\frac{1}{3}$ |
11.菱形具有而矩形不一定具有的性质是( )
| A. | 两组对边分别平行 | B. | 对角线相等 | ||
| C. | 对角线互相平分 | D. | 四条边相等 |
 如图,Rt△ABC中,∠C=90°,且AC=1,BC=2,则sin∠A=$\frac{2\sqrt{5}}{5}$.
如图,Rt△ABC中,∠C=90°,且AC=1,BC=2,则sin∠A=$\frac{2\sqrt{5}}{5}$.