题目内容
12.解下列方程组.(1)$\left\{\begin{array}{l}{x+2y=4}\\{2x-3y=1}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x+4y=14}\\{\frac{x-3}{4}-\frac{y-3}{3}=\frac{1}{12}}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x+2y=4①}\\{2x-3y=1②}\end{array}\right.$,
①×2-②得:7y=7,即y=1,
把y=1代入①得:x=2,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{x+4y=14①}\\{3x-4y=-2②}\end{array}\right.$,
①+②得:4x=12,即x=3,
把x=3代入①得:y=$\frac{11}{4}$,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=\frac{11}{4}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
1.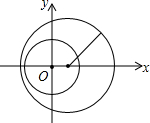 如图,小圆的圆心在原点,半径为3,大圆的圆心坐标为(a,0)半径为5.如果两圆内含,那么a的取值范围为( )
如图,小圆的圆心在原点,半径为3,大圆的圆心坐标为(a,0)半径为5.如果两圆内含,那么a的取值范围为( )
 如图,小圆的圆心在原点,半径为3,大圆的圆心坐标为(a,0)半径为5.如果两圆内含,那么a的取值范围为( )
如图,小圆的圆心在原点,半径为3,大圆的圆心坐标为(a,0)半径为5.如果两圆内含,那么a的取值范围为( )| A. | -2≤a≤2 | B. | -2<a<2 | C. | 0<a<5 | D. | 0<a<3 |
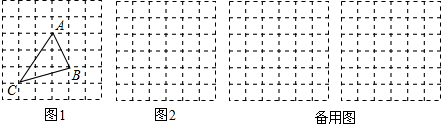
 如图,DE∥BC,∠D=120°,∠1=∠2,求∠DEB的度数.
如图,DE∥BC,∠D=120°,∠1=∠2,求∠DEB的度数.