题目内容
17.已知y-1和3-2x互为相反数,且x-y+4的平方根是它本身,求x、y的值.分析 根据互为相反数两数之和为0,且平方根等于本身的数为0,列出方程组,求出方程组的解即可得到x与y的值.
解答 解:根据题意得:$\left\{\begin{array}{l}{y-1+3-2x=0}\\{x-y+4=0}\end{array}\right.$,
整理得:$\left\{\begin{array}{l}{2x-y=2①}\\{x-y=-4②}\end{array}\right.$,
①-②得:x=6,
把x=6代入②得:y=10,
则方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=10}\end{array}\right.$.
点评 此题考查了解二元一次方程组,相反数,以及平方根,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
8. 某校为了解七年级学生课外学习情况,随机抽取了部分学生作调查,通过调查将获得的数据按性别绘制成如下的女生频数分布表和如图所示的男生频数分布直方图:
某校为了解七年级学生课外学习情况,随机抽取了部分学生作调查,通过调查将获得的数据按性别绘制成如下的女生频数分布表和如图所示的男生频数分布直方图:
根据图表解答下列问题:
(1)在女生的频数分布表中,m=3,n=20%;
(2)此次调查共抽取了多少名学生?
(3)从学习时间在120~150分钟的5名学生中依次抽取两名学生调查学习效率,恰好抽到男女生各一名的概率是多少?
 某校为了解七年级学生课外学习情况,随机抽取了部分学生作调查,通过调查将获得的数据按性别绘制成如下的女生频数分布表和如图所示的男生频数分布直方图:
某校为了解七年级学生课外学习情况,随机抽取了部分学生作调查,通过调查将获得的数据按性别绘制成如下的女生频数分布表和如图所示的男生频数分布直方图:| 学习时间t(分钟) | 人数 | 占女生人数百分比 |
| 0≤t<30 | 4 | 20% |
| 30≤t<60 | m | 15% |
| 60≤t<90 | 5 | 25% |
| 90≤t<120 | 6 | n |
| 120≤t<150 | 2 | 10% |
(1)在女生的频数分布表中,m=3,n=20%;
(2)此次调查共抽取了多少名学生?
(3)从学习时间在120~150分钟的5名学生中依次抽取两名学生调查学习效率,恰好抽到男女生各一名的概率是多少?
5.若x2+2(m-3)x+16是完全平方式,则m的值是( )
| A. | -1 | B. | 7 | C. | -1 或7 | D. | 1或5 |
6.关于x的方程ax2+bx+c=0(a≠0)有两个相等的实数根,则$\frac{{b}^{2}}{{b}^{2}-ac}$的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
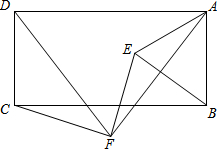 如图:F是矩形ABCD下方一点,将△FCD绕F点顺时针旋转60°后,恰好D点与A点重合,得到△FEA,连结EB得到△ABE,猜想并证明△ABE的形状.
如图:F是矩形ABCD下方一点,将△FCD绕F点顺时针旋转60°后,恰好D点与A点重合,得到△FEA,连结EB得到△ABE,猜想并证明△ABE的形状. 如图,已知△ABC和点O,以点O为位似中心,求作△ABC的位似图形,使它与△ABC的相似比为$\frac{1}{2}$.
如图,已知△ABC和点O,以点O为位似中心,求作△ABC的位似图形,使它与△ABC的相似比为$\frac{1}{2}$.