Question

16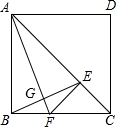．如图，点E是正方形ABCD的对角线AC上的一个动点（不与A、C重合），作EF⊥AC交边BC于点F，联结AF、BE交于点G．
（1）求证：△CAF∽△CBE；
（2）若AE：EC=2：1，求tan∠BEF的值．

Answer 1

分析 （1）利用AA证明△CEF∽△CAB，再列出比例式利用SAS证明△CAF∽△CBE
（2）证出∴∠BAF=∠BEF，设EC=1，则EF=1，FC=$\sqrt{2}$，AC=3，由勾股定理得出AB=BC=$\frac{\sqrt{2}}{2}$AC=$\frac{3\sqrt{2}}{2}$，得出BF=BC-FC=$\frac{\sqrt{2}}{2}$，由三角函数即可得出结果．

解答 （1）证明：∵四边形ABCD是正方形，
∴∠ABC=90°，
∵EF⊥AC，
∴∠FEC=90°=∠ABC，
又∵∠FCE=∠ACB，
∴△CEF∽△CAB，
∴$\frac{CF}{CE}=\frac{CB}{CA}$，
又∵∠ACF=∠BCE，
∴△CAF∽△CBE；
（2）∵△CAF∽△CBE，
∴∠CAF=∠CBE，
∵∠BAC=∠BCA=45°，
∴∠BAF=∠BEF，
设EC=1，则EF=1，FC=$\sqrt{2}$，
∵AE：EC=2：1，
∴AC=3，
∴AB=BC=$\frac{\sqrt{2}}{2}$AC=$\frac{3\sqrt{2}}{2}$，
∴BF=BC-FC=$\frac{\sqrt{2}}{2}$，
∴tan∠BEF=tan∠BAF=$\frac{BF}{AB}$=$\frac{1}{3}$．

点评 本题考查了正方形的性质、相似三角形的判定与性质、勾股定理、三角函数等知识；熟练掌握正方形的性质，证明三角形相似是解决问题的关键．