题目内容
11．数学小组在活动中继承了学兄学姐们的研究成果，将能够确定形如y=ax2+bx+c的抛物线的形状、大小、开口方向、位置等特征的系数a、b、c称为该抛物线的特征数，记作：特征数{a、b、c}，（请你求）在研究活动中被记作特征数为{1、-4、3}的抛物线的顶点坐标为（2，-1）．分析 由条件可求得抛物线解析式，化为顶点式可求得答案．
解答 解：
∵特征数为{1、-4、3}，
∴抛物线解析式为y=x2-4x+3=（x-2）2-1，
∴抛物线顶点坐标为（2，-1），
故答案为：（2，-1）．
点评 本题主要考查二次函数的性质，掌握抛物线的顶点式是解题的关键，即在y=a（x-h）2+k中，对称轴为x=h，顶点坐标为（h，k）．
练习册系列答案
相关题目
如图，E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为点C和点D．
19．已知∠A=30°，下列判断正确的是（ ）
| A． | sinA=$\frac{1}{2}$ | B． | cosA=$\frac{1}{2}$ | C． | tanA=$\frac{1}{2}$ | D． | cotA=$\frac{1}{2}$ |
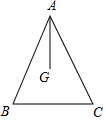如图，G为△ABC的重心，如果AB=AC=13，BC=10，那么AG的长为8．
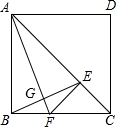如图，点E是正方形ABCD的对角线AC上的一个动点（不与A、C重合），作EF⊥AC交边BC于点F，联结AF、BE交于点G．