题目内容
5．已知一斜坡的坡度i=1：2，高度在20米，那么这一斜坡的坡长约为44.7米（精确到0.1米）分析 根据题意画出图形，由斜坡的坡度i=1：2可设BC=x，则AC=2x，由勾股定理得出AB的长，再由BC=20米即可得出结论．
解答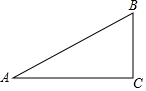 
解：如图，∵斜坡的坡度i=1：2，
∴设BC=x，则AC=2x，
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{x}^{2}+4{x}^{2}}$=$\sqrt{5}$x，
∴$\frac{BC}{AB}$=$\frac{x}{\sqrt{5}x}$．
∵BC=20米，
∴$\frac{x}{\sqrt{5}x}$=$\frac{20}{AB}$，解得x=20$\sqrt{5}$≈44.7（米）．
故答案为：44.7．
点评 本题考查的是解直角三角形的应用-坡度坡脚问题，熟记锐角三角函数的定义是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
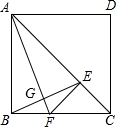如图，点E是正方形ABCD的对角线AC上的一个动点（不与A、C重合），作EF⊥AC交边BC于点F，联结AF、BE交于点G．
如图，在平面直角坐标系中xOy中，抛物线y=-x2+bx+c与x轴相交于点A（-1，0）和点B，与y轴相交于点C（0，3），抛物线的顶点为点D，联结AC、BC、DB、DC．
图中有几个三角形？用符号表示这些三角形．