题目内容
4．
如图，△ABC中∠C=90°，若CD⊥AB于D，且BD=4，AD=9，则tanA=$\frac{2}{3}$．
分析 先证明△BDC∽△CDA，利用相似三角形的性质求出CD的长度，然后根据锐角三角函数的定义即可求出tanA的值．
解答 解：∵∠BCD+∠DCA=∠DCA+∠A=90°，
∴∠BCD=∠A，
∵CD⊥AB，
∴∠BDC=∠CDA=90°，
∴△BDC∽△CDA，
∴CD2=BD•AD，
∴CD=6，
∴tanA=$\frac{CD}{AD}$=$\frac{2}{3}$
故答案为：$\frac{2}{3}$
点评 本题考查解直角三角形，涉及锐角三角函数，相似三角形的判定与性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．已知∠A=30°，下列判断正确的是（ ）
| A． | sinA=$\frac{1}{2}$ | B． | cosA=$\frac{1}{2}$ | C． | tanA=$\frac{1}{2}$ | D． | cotA=$\frac{1}{2}$ |
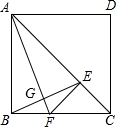如图，点E是正方形ABCD的对角线AC上的一个动点（不与A、C重合），作EF⊥AC交边BC于点F，联结AF、BE交于点G．
如图，在平面直角坐标系中xOy中，抛物线y=-x2+bx+c与x轴相交于点A（-1，0）和点B，与y轴相交于点C（0，3），抛物线的顶点为点D，联结AC、BC、DB、DC．