题目内容
13.抛物线y=ax2+bx+3(a≠0)过A(4,4),B (2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是m≤3或m≥4.分析 把A(4,4)代入抛物线y=ax2+bx+3得4a+b=$\frac{1}{4}$,根据对称轴x=-$\frac{b}{2a}$,B(2,m),且点B到抛物线对称轴的距离记为d,满足0<d≤1,所以0<|2-(-$\frac{b}{2a}$)|≤1,解得a≥$\frac{1}{8}$或a≤-$\frac{1}{8}$,把B(2,m)代入y=ax2+bx+3得:4a+2b+3=m,得到a=$\frac{7}{8}$-$\frac{m}{4}$,所以$\frac{7}{8}$-$\frac{m}{4}$≥$\frac{1}{8}$或$\frac{7}{8}$-$\frac{m}{4}$≤-$\frac{7}{8}$,即可解答.
解答 解:把A(4,4)代入抛物线y=ax2+bx+3得:
16a+4b+3=4,
∴16a+4b=1,
∴4a+b=$\frac{1}{4}$,
∵对称轴x=-$\frac{b}{2a}$,B(2,m),且点B到抛物线对称轴的距离记为d,满足0<d≤1,
∴0$<|2-(-\frac{b}{2a})|$≤1,
∴0<$\frac{4a+b}{2a}$≤1,
∴|$\frac{1}{8a}$|≤1,
∴a≥$\frac{1}{8}$或a≤-$\frac{1}{8}$,
把B(2,m)代入y=ax2+bx+3得:
4a+2b+3=m
2(2a+b)+3=m
2(2a+$\frac{1}{4}$-4a)+3=m
∴a=$\frac{7}{8}$-$\frac{m}{4}$,
∴$\frac{7}{8}$-$\frac{m}{4}$≥$\frac{1}{8}$或$\frac{7}{8}$-$\frac{m}{4}$≤-$\frac{7}{8}$,
∴m≤3或m≥4.
故答案为:m≤3或m≥4.
点评 本题考查了二次函数的性质,解决本题的关键是根据点B到抛物线对称轴的距离记为d,满足0<d≤1,得到0<|2-(-$\frac{b}{2a}$)|≤1.

| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |

| A. | B与C | B. | C与D | C. | E与F | D. | A与B |
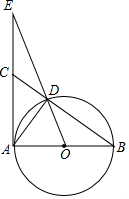 已知,如图,Rt△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于D,OD交AC的延长线于E,OA=1,AE=3.则下列结论正确的有①③④.
已知,如图,Rt△ABC中,∠BAC=90°,以AB为直径的⊙O交BC于D,OD交AC的延长线于E,OA=1,AE=3.则下列结论正确的有①③④.