题目内容
3.某村老杨家有耕地和林地共24公顷,今年每公顷耕地纯收入为5500元,每公顷林地纯收入为6000元,耕地与林地的纯收入共137000元,为保护生态环境,增加收入,老杨计划将部分耕地改为林地(改后每公顷耕地,林地纯收入不变),要使改后的纯收入为140000元.问:(1)老杨家原有耕地,林地各多少公顷?
(2)老杨应将多少公顷耕地改为林地?
分析 (1)设老杨家原有耕地x公顷,老杨家原有林地y公顷,根据耕地和林地的总数量结合年纯收入为137000元,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设老杨应将m公顷耕地改为林地,则更改后林地的面积为(10+m)公顷,耕地的面积为(14-m),根据更改后的纯收入为140000元,即可得出关于m的一元一次方程,解之即可得出结论.
解答 解:(1)设老杨家原有耕地x公顷,老杨家原有林地y公顷,
根据题意得:$\left\{\begin{array}{l}{x+y=24}\\{5500x+6000y=137000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=14}\\{y=10}\end{array}\right.$.
答:老杨家原有耕地14公顷,老杨家原有林地10公顷.
(2)设老杨应将m公顷耕地改为林地,则更改后林地的面积为(10+m)公顷,耕地的面积为(14-m),
根据题意得:5500(14-m)+6000(10+m)=140000,
解得:m=6.
答:老杨应将6公顷耕地改为林地.
点评 本题考查了二元一次方程组的应用以及一元一次方程的应用,解题的关键是:(1)根据耕地和林地的总数量结合年纯收入为137000元,列出关于x、y的二元一次方程组;(2)根据更改后的纯收入为140000元,列出关于m的一元一次方程.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
6. 如图,AB∥CD,∠A=50°,∠C=30°,则∠AEC等于( )
如图,AB∥CD,∠A=50°,∠C=30°,则∠AEC等于( )
 如图,AB∥CD,∠A=50°,∠C=30°,则∠AEC等于( )
如图,AB∥CD,∠A=50°,∠C=30°,则∠AEC等于( )| A. | 20° | B. | 50° | C. | 80° | D. | 100° |
 如图是一个圆柱体和一个长方体组成的几何体,圆柱的下底面紧贴在长方体的上底面上,那么这个几何体的俯视图为( )
如图是一个圆柱体和一个长方体组成的几何体,圆柱的下底面紧贴在长方体的上底面上,那么这个几何体的俯视图为( )



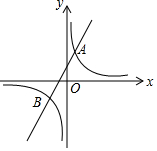 已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).