题目内容
6.如果$\frac{x+y}{y}$=$\frac{7}{4}$,那么$\frac{x}{y}$的值是$\frac{3}{4}$.分析 根据$\frac{x+y}{y}$=$\frac{7}{4}$,应用比例的性质,求出$\frac{x}{y}$的值是多少即可.
解答 解:∵$\frac{x+y}{y}$=$\frac{7}{4}$,
∴$\frac{x}{y}$=$\frac{7-4}{4}$=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 此题主要考查了比例的性质和应用,要熟练掌握.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
16.如图是一个运算程序,若输出的值为8,则输入值x是( )


| A. | 5 | B. | 8 | C. | 16 | D. | 5或16 |
17. 如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD,下列结论:①EG丄FH; ②四边形EFGH是矩形;③HF平分∠EHG:④四边形EFGH是菱形,其中正确的结论有( )个.
如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD,下列结论:①EG丄FH; ②四边形EFGH是矩形;③HF平分∠EHG:④四边形EFGH是菱形,其中正确的结论有( )个.
 如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD,下列结论:①EG丄FH; ②四边形EFGH是矩形;③HF平分∠EHG:④四边形EFGH是菱形,其中正确的结论有( )个.
如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD,下列结论:①EG丄FH; ②四边形EFGH是矩形;③HF平分∠EHG:④四边形EFGH是菱形,其中正确的结论有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.下列说法:①球有1个面;②同一平面内的两点,可以确定一条直线;③两点之间,线段最短;④射线没有端点,其中不正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.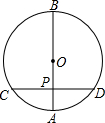 如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )
如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )
 如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )
如图,在⊙O中,直径AB垂直于弦CD,垂足为P,若PA=4,PB=12,则CP的长为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 8 | D. | 4$\sqrt{3}$ |
11.反比例函数y=$\frac{k}{x}$的图象生经过点(1,-2),则k的值为( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
18. 如图是一个正方体的包装盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A,B,C内的三个数依次是( )
如图是一个正方体的包装盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A,B,C内的三个数依次是( )
 如图是一个正方体的包装盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A,B,C内的三个数依次是( )
如图是一个正方体的包装盒的展开图,若在其中的三个正方形A,B,C内分别填上适当的数,使得将这个展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A,B,C内的三个数依次是( )| A. | 2,1,-2 | B. | -1,2,-2 | C. | -1,-2,2 | D. | -2,1,2 |
15.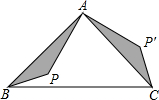 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 8 |
16.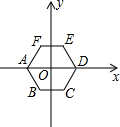 如图,以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系,顶点A,D在x轴上,则点C的坐标为( )
如图,以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系,顶点A,D在x轴上,则点C的坐标为( )
 如图,以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系,顶点A,D在x轴上,则点C的坐标为( )
如图,以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系,顶点A,D在x轴上,则点C的坐标为( )| A. | (1,-2) | B. | (1,-$\sqrt{2}$) | C. | (1,-$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$) |