题目内容
18．如图1，在矩形ABCD中，动点P从点B出发，沿BC、CD运动至点D停止．设点P运动的路程为x，△ABP的面积为y．如果y关于x的函数图象如图2所示，则BD的长是（ ）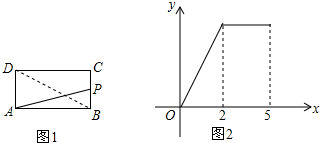
| A． | $\sqrt{13}$ | B． | $\sqrt{29}$ | C． | $\sqrt{10}$ | D． | 3 |
分析 根据题意，分析P的运动路线，分2个阶段分别讨论，可得BC与CD的值，进而利用勾股定理可得答案．
解答 解：根据题意，
当P在BC上时，三角形面积增大，结合图2可得，BC=2；
当P在CD上时，三角形面积不变，结合图2可得，CD=3；
因此BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{13}$．
故选：A．
点评 本题主要考查了动点问题的函数图象，在解题时要能根据函数的图象求出有关的线段的长度，从而利用勾股定理解决问题．
练习册系列答案
相关题目
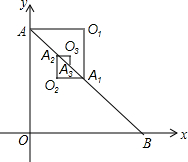如图，在Rt△AOB中，OA=OB=1，取AB的中点A1，以AA1为斜边作等腰直角三角形AO1A1，取AA1的中点A2，以A1A2为斜边作等腰直角三角形A1O2A1；取A1A2的中点A3，以A2A3为斜边作等腰直角三角形A2O3A3…，则点O6的坐标是（$\frac{21}{64}$，$\frac{21}{32}$）．
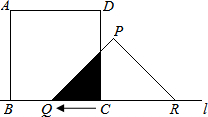如图，有一边长为5cm的正方形ABCD和等腰Rt△PQR，QR=8cm，点B、C、Q、R在同一条直线上，当C、Q两点重合时，△PQR以1cm/秒的速度向左开始匀速运动，设与正方形重合部分的面积为S cm2．
10．某电脑公司准备每周（按120个工时计算）组装三种型号的电脑360台，组装这些电脑每台所需工时和每台产值如下表．
（1）如果每周准备组装100台型号③电脑，那么每周应组装型号①、②电脑各几台？
（2）如果一周产值定为10万元，那么这周应组装型号①、②、③电脑各几台？
（3）若一周型号③电脑至少组装20台，一周产值记为w，试直接写出w的范围．
| 电脑型号 | ① | ② | ③ |
| 工时（个） | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
| 产值（万元） | 0.4 | 0.3 | 0.2 |
（2）如果一周产值定为10万元，那么这周应组装型号①、②、③电脑各几台？
（3）若一周型号③电脑至少组装20台，一周产值记为w，试直接写出w的范围．
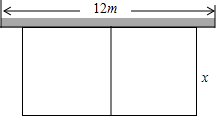有长24m的篱笆，一面利用长为12m的围墙围成如图所示中间隔有一道篱笆的矩形花圃．设花圃垂直于墙的一边长为xm，面积为Sm2．则S与x的函数关系式是S=（24-3x）x，x的取值范围为4≤x＜8．