题目内容
6.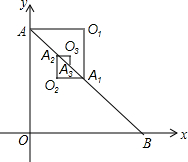 如图,在Rt△AOB中,OA=OB=1,取AB的中点A1,以AA1为斜边作等腰直角三角形AO1A1,取AA1的中点A2,以A1A2为斜边作等腰直角三角形A1O2A1;取A1A2的中点A3,以A2A3为斜边作等腰直角三角形A2O3A3…,则点O6的坐标是($\frac{21}{64}$,$\frac{21}{32}$).
如图,在Rt△AOB中,OA=OB=1,取AB的中点A1,以AA1为斜边作等腰直角三角形AO1A1,取AA1的中点A2,以A1A2为斜边作等腰直角三角形A1O2A1;取A1A2的中点A3,以A2A3为斜边作等腰直角三角形A2O3A3…,则点O6的坐标是($\frac{21}{64}$,$\frac{21}{32}$).
分析 求出O1,O2,O3的坐标发现规律,可求出点O6的坐标.
解答 解:O1($\frac{1}{2}$,1),O2($\frac{1}{4}$,$\frac{1}{2}$)O3($\frac{3}{8}$,$\frac{3}{4}$),不难发现O3的横坐标为$\frac{3}{8}$=$\frac{1}{2}$×($\frac{1}{2}+\frac{1}{4}$),O3的纵坐标为$\frac{3}{4}$=$\frac{1}{2}$×(1+$\frac{1}{2}$),于是On的横坐标为On-1、On-2的横坐标和的一半,On的纵坐标为On-1、On-2的纵坐标和的一半,
所以O4($\frac{5}{16}$,$\frac{5}{8}$),O5($\frac{11}{32}$,$\frac{11}{16}$),O6($\frac{21}{64}$,$\frac{21}{32}$).
故答案为:($\frac{21}{64}$,$\frac{21}{32}$).
点评 本题考查了点的坐标问题,先从几个简单点入手发现规律,然后根据得出的规律求值.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.为了满足市场需求,某厂家生产A、B两款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产A种购物袋x个.
(1)每天的生产成本是多少?
(2)每天获得的利润是多少(利润=售价-成本)(上两问均用舍x的式子表示,并将所列的式子进行化简)
(3)当x=2000时,求一个月(按30天算)的总利润是多少?
| 成本(元/个) | 售价 (元/个) | |
| A | 2 | 2.4 |
| B | 3 | 3.6 |
(2)每天获得的利润是多少(利润=售价-成本)(上两问均用舍x的式子表示,并将所列的式子进行化简)
(3)当x=2000时,求一个月(按30天算)的总利润是多少?
18.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y.如果y关于x的函数图象如图2所示,则BD的长是( )
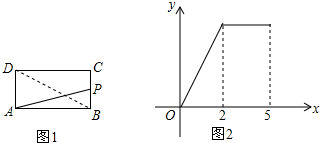

| A. | $\sqrt{13}$ | B. | $\sqrt{29}$ | C. | $\sqrt{10}$ | D. | 3 |
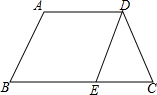 如图,已知梯形ABCD中,AD∥BC,AB=DC,AB<AD,BC<2AD,DE∥AB,在以图中字母标注的点为起点和终点的有向线段中,将满足以下各题所列条件的所有有向线段用符号表示出来.
如图,已知梯形ABCD中,AD∥BC,AB=DC,AB<AD,BC<2AD,DE∥AB,在以图中字母标注的点为起点和终点的有向线段中,将满足以下各题所列条件的所有有向线段用符号表示出来. 如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D为抛物线的顶点,点P为第一象限抛物线上一点,且∠DAP=45°,求点P的坐标.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D为抛物线的顶点,点P为第一象限抛物线上一点,且∠DAP=45°,求点P的坐标. 如图,用钢筋做支架,要求BA,DC相交所成的锐角为32°,现测得∠BAC=∠DCA=115°,则这个支架符合设计要求吗?为什么?
如图,用钢筋做支架,要求BA,DC相交所成的锐角为32°,现测得∠BAC=∠DCA=115°,则这个支架符合设计要求吗?为什么?