题目内容
7.若(2xmy3)2与-(x2y2n)3是同类项,求(m-2n)(2m+n)-m(2m-3n-1)的值.分析 首先利用积的乘方计算,再利用同类项的意义求得m、n的数值,进一步利用整式的乘法计算化简,最后代入求得数值即可.
解答 解:∵(2xmy3)2=42my6,-(x2y2n)3=-x6y6n是同类项,
∴m=3,n=1,
∴(m-2n)(2m+n)-m(2m-3n-1)
=2m2-3mn-2n2-2m2+6mn+m
=-2n2+3mn+m
=-2+9+3
=10.
点评 此题考查整式的混合运算与化简求值,同类项的意义,掌握整式混合运算的计算方法和同类项的意义是解决问题的关键.

练习册系列答案
相关题目
18.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y.如果y关于x的函数图象如图2所示,则BD的长是( )
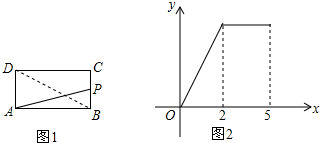

| A. | $\sqrt{13}$ | B. | $\sqrt{29}$ | C. | $\sqrt{10}$ | D. | 3 |
 如图,用钢筋做支架,要求BA,DC相交所成的锐角为32°,现测得∠BAC=∠DCA=115°,则这个支架符合设计要求吗?为什么?
如图,用钢筋做支架,要求BA,DC相交所成的锐角为32°,现测得∠BAC=∠DCA=115°,则这个支架符合设计要求吗?为什么? 如图,在等腰△ABC中,AB=AC=13,BC=10,D是BC边上的中点,M、N分别是AD和AB上的动点.则BM+MN的最小值是$\frac{120}{13}$.
如图,在等腰△ABC中,AB=AC=13,BC=10,D是BC边上的中点,M、N分别是AD和AB上的动点.则BM+MN的最小值是$\frac{120}{13}$.