题目内容
3.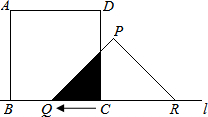 如图,有一边长为5cm的正方形ABCD和等腰Rt△PQR,QR=8cm,点B、C、Q、R在同一条直线上,当C、Q两点重合时,△PQR以1cm/秒的速度向左开始匀速运动,设与正方形重合部分的面积为S cm2.
如图,有一边长为5cm的正方形ABCD和等腰Rt△PQR,QR=8cm,点B、C、Q、R在同一条直线上,当C、Q两点重合时,△PQR以1cm/秒的速度向左开始匀速运动,设与正方形重合部分的面积为S cm2.(1)求S与运动时间t(秒)的函数关系式,并指出自变量的取值范围;
(2)求S的最大值.
分析 (1)画出图形,按照不同的运动时间,分类探讨得出S与运动时间t(秒)的函数关系式,进一步求得最大值;
(2)比较(1)中的不同取值范围内的最大值,得出答案即可.
解答 解:(1)①如图,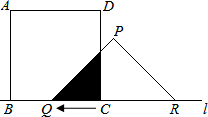
当0≤t≤4时,S=$\frac{1}{2}$CQ2=$\frac{1}{2}$t2,
当t=4时,S最大为8;
②如图,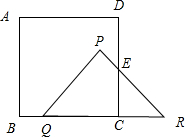
当4<t≤5时,S=S△PQR-S△ECR,
CR=8-CQ=8-t=CE,
S=$\frac{1}{2}$×8×4-$\frac{1}{2}$(8-t)2═-$\frac{1}{2}$(t-8)2-16=-$\frac{1}{2}$(t-8)2+16,
当t=5时,S最大为$\frac{23}{2}$;
③如图,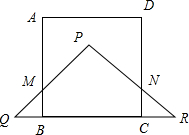
当5≤t≤8时,S=S△PQR-S△BMQ-S△NCR,
BQ=t-5,CR=8-t,
S=$\frac{1}{2}$×8×4-$\frac{1}{2}$(t-5)2-$\frac{1}{2}$(8-t)2=-$\frac{1}{2}$t2+8t-$\frac{57}{2}$=-$\frac{1}{2}$(t-$\frac{13}{2}$)2+$\frac{55}{4}$,
当t=$\frac{13}{2}$时,S最大为$\frac{55}{4}$;
④如图,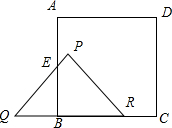
当8≤t≤9时,S=S△PQR-S△BEQ,
BQ=t-5,CR=
S=$\frac{1}{2}$×8×4-$\frac{1}{2}$(t-5)2=-$\frac{1}{2}$t2+5t+$\frac{7}{2}$=-$\frac{1}{2}$(t-5)2+16,
当t=8时,S最大为$\frac{23}{2}$;
⑤如图,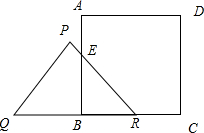
当9≤t≤13时,S=S△BER,
BR=8-(t-5)=13-t,
S=$\frac{1}{2}$(13-t)2,
当t=9时,S最大为8;
⑥当t>13,S=0;
(2)由(1)可知:S的最大值是$\frac{55}{4}$.
点评 此题考查动点问题与函数,根据正方形ABCD的边长和等腰Rt△PQR的底边长结合运动速度,按照不同的取值范围分类探讨是解决问题的难点.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
| A. | $\sqrt{13}$ | B. | $\sqrt{29}$ | C. | $\sqrt{10}$ | D. | 3 |
| A. | 第一,二,三象限 | B. | x轴上方 | C. | x轴下方 | D. | 第二,三,四象限 |
 如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D为抛物线的顶点,点P为第一象限抛物线上一点,且∠DAP=45°,求点P的坐标.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D为抛物线的顶点,点P为第一象限抛物线上一点,且∠DAP=45°,求点P的坐标.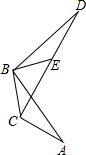 △ABC绕点B逆时针旋转90°得到△DBE,若恰好得到C,E,D三点共线,则AC、BC、CD的数量关系是$\sqrt{2}$BC+AC=CD.
△ABC绕点B逆时针旋转90°得到△DBE,若恰好得到C,E,D三点共线,则AC、BC、CD的数量关系是$\sqrt{2}$BC+AC=CD.