题目内容
若一元二次方程(m-1)x2+(m2+1)x+m2-1=0的常数项为0,则m的值为( )
| A、1 | B、-1 | C、±1 | D、0 |
考点:一元二次方程的一般形式,一元二次方程的定义
专题:计算题
分析:令常数项为0求出m的值,代入检验即可.
解答:解:∵一元二次方程(m-1)x2+(m2+1)x+m2-1=0的常数项为0,
∴m2-1=0,即m=1或-1,
当m=1时,m-1=0,不合题意,舍去,
则m=-1,
故选B
∴m2-1=0,即m=1或-1,
当m=1时,m-1=0,不合题意,舍去,
则m=-1,
故选B
点评:此题考查了一元二次方程的一般形式,一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知在⊙O中,半径r=13,弦AB∥CD,且AB=24,CD=10,则AB与CD的距离为( )
| A、5 | B、7 | C、17 | D、7或17 |
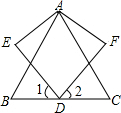 如图,△ABC中,AB=AC,D是BC的中点,∠AED=∠AFD=90°,AE=AF.
如图,△ABC中,AB=AC,D是BC的中点,∠AED=∠AFD=90°,AE=AF.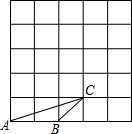 如图,在5×5的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上,作一个与△ABC相似的△DEF,使它的三个顶点都在小正方形的顶点上,则△DEF的最大面积是
如图,在5×5的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上,作一个与△ABC相似的△DEF,使它的三个顶点都在小正方形的顶点上,则△DEF的最大面积是 已知y+2与x成正比例,且x=-2时,y=0.
已知y+2与x成正比例,且x=-2时,y=0.