题目内容
19.有理数a,b,c都不为零,且a+b+c=0,则$\frac{|b+c|}{a}$+$\frac{|a+c|}{b}$+$\frac{|a+b|}{c}$=( )| A. | 1 | B. | ±1 | C. | -1 | D. | 0 |
分析 根据a、b、c是非零有理数,且a+b+c=0,可知a,b,c为两正一负或两负一正,按两种情况分别讨论,求得代数式的可能的取值即可.
解答 解解:∵a、b、c是非零有理数,且a+b+c=0,
∴a,b,c为两正一负或两负一正,且b+c=-a,a+c=-b,a+b=-c,
①当a>b>0>c时:$\frac{|b+c|}{a}$+$\frac{|a+c|}{b}$+$\frac{|a+b|}{c}$=$\frac{|-a|}{a}$+$\frac{|-b|}{b}$+$\frac{|-c|}{c}$=1+1-1=1;
②当a>0>b>c时:$\frac{|b+c|}{a}$+$\frac{|a+c|}{b}$+$\frac{|a+b|}{c}$=$\frac{|-a|}{a}$+$\frac{|-b|}{b}$+$\frac{|-c|}{c}$=1-1-1=-1;
综上,$\frac{|b+c|}{a}$+$\frac{|a+c|}{b}$+$\frac{|a+b|}{c}$的所有可能的值为±1.
故选(B)
点评 本题主要考查了代数式求值,关键是掌握绝对值的性质等知识点,注意分情况讨论字母的符号,不要漏解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.2015年12月9日德国《柏林日报》报道,全球各地销售的近四分之三的玩具都是由中国工厂生产的,若中国某玩具工厂生产了一批玩具共3000个,为检测该批玩具的质量是否合格,质检人员从中随机抽查了300个,合格的有290个,在此次调查中,所抽取的300个玩具的合格情况是( )
| A. | 总体 | B. | 个体 | C. | 样本 | D. | 样本容量 |
10.某区在改善环境绿化方面,将投入资金由计划的1500000元提高到2000000元.其中2000000用科学记数法表示为( )
| A. | 0.2×107 | B. | 2×107 | C. | 20×105 | D. | 2×106 |
7.数据0.0000314用科学记数法表示为( )
| A. | 3.14×10-5 | B. | 31.44×10-4 | C. | 3.14×10-6 | D. | 0.314×10-6 |
9.关于x的不等式组$\left\{\begin{array}{l}{2x-1≤11}\\{x+1>a}\end{array}\right.$恰好只有两个整数解,则a的取值范围为( )
| A. | 5≤a<6 | B. | 5<a≤6 | C. | 4≤a<6 | D. | 4<a≤6 |
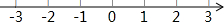 解不等式组$\left\{\begin{array}{l}3x-1<2(x+1)\\-\frac{x}{3}≤\frac{5x}{3}+2\end{array}\right.$并在数轴上表示出解集.
解不等式组$\left\{\begin{array}{l}3x-1<2(x+1)\\-\frac{x}{3}≤\frac{5x}{3}+2\end{array}\right.$并在数轴上表示出解集.