题目内容
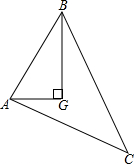 如图所示,点G是△ABC的重心,GA⊥GB,AB=5,则AC2+BC2的值为
如图所示,点G是△ABC的重心,GA⊥GB,AB=5,则AC2+BC2的值为考点:三角形的重心
专题:计算题
分析:延长AG交BC于E,延长BG交AC于D,如图,根据重心的定义得到AD=
AC,BE=
BC,再利用勾股定理得AD2=AG2+GD2,BE2=BG2+GE2,则AD2+BE2=AG2+GD2+BG2+GE2,再根据重心的性质得GD=
BG,GE=
AG,所以AD2+BE2=
(AG2+BG2)=
•AB2=
,于是AC2+BC2=4AD2+4BE2=125.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
| 125 |
| 4 |
解答:解:延长AG交BC于E,延长BG交AC于D,如图,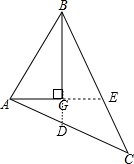
∵点G是△ABC的重心,
∴AE和BD为△ABC的中线,即AD=
AC,BE=
BC,
∵GA⊥GB,
∴∠AGB=90°,
在Rt△AGD中,AD2=AG2+GD2,
在Rt△BGE中,BE2=BG2+GE2,
∴AD2+BE2=AG2+GD2+BG2+GE2,
∵点G是△ABC的重心,
∴GD=
BG,GE=
AG,
∴AD2+BE2=AG2+
BG2+BG2+
AG2
=
(AG2+BG2)
=
•AB2
=
•25
=
,
∴AC2+BC2=4AD2+4BE2=4•
=125.
故答案为125.

∵点G是△ABC的重心,
∴AE和BD为△ABC的中线,即AD=
| 1 |
| 2 |
| 1 |
| 2 |
∵GA⊥GB,
∴∠AGB=90°,
在Rt△AGD中,AD2=AG2+GD2,
在Rt△BGE中,BE2=BG2+GE2,
∴AD2+BE2=AG2+GD2+BG2+GE2,
∵点G是△ABC的重心,
∴GD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD2+BE2=AG2+
| 1 |
| 4 |
| 1 |
| 4 |
=
| 5 |
| 4 |
=
| 5 |
| 4 |
=
| 5 |
| 4 |
=
| 125 |
| 4 |
∴AC2+BC2=4AD2+4BE2=4•
| 125 |
| 4 |
故答案为125.
点评:本题考查了三角形的重心:三角形的重心是三角形三边中线的交点.重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查了勾股定理.

练习册系列答案
相关题目
当x>1时,|x-1|+2|1-x|+|x|的值为( )
| A、3-4x | B、4x-3 |
| C、3-2x | D、1 |
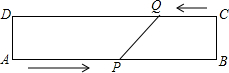 如图,在矩形ABCD中,AB=20 cm,动点P从点A开始沿AB边以4 cm/s的速度运动,动点Q从点C开始沿CD边以1 cm/s的速度运动,点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动,运动点的运动时间为t s,则当t为何值时,四边形APQD时矩形?
如图,在矩形ABCD中,AB=20 cm,动点P从点A开始沿AB边以4 cm/s的速度运动,动点Q从点C开始沿CD边以1 cm/s的速度运动,点P和点Q同时出发,当其中一点到达终点时,另一点也随之停止运动,运动点的运动时间为t s,则当t为何值时,四边形APQD时矩形?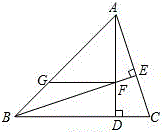 已知在△ABC中,∠ABC=45°,高AD所在的直线与高BE所在的直线交于点F,过点F作GF∥BC,交直线AB于点G,连接CF.
已知在△ABC中,∠ABC=45°,高AD所在的直线与高BE所在的直线交于点F,过点F作GF∥BC,交直线AB于点G,连接CF. 正方形ABCD与正方形DEFG的边长分别是8和5,E在AD的延长线上,G在CD的延长线上,求△ACF的面积.
正方形ABCD与正方形DEFG的边长分别是8和5,E在AD的延长线上,G在CD的延长线上,求△ACF的面积. 如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠AEF,若∠1=38°,求∠2的度数.
如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠AEF,若∠1=38°,求∠2的度数. 如图,已知AB∥CD,GH是直线,∠1+∠2=180°,问CD与EF是否平行?为什么?
如图,已知AB∥CD,GH是直线,∠1+∠2=180°,问CD与EF是否平行?为什么?