题目内容
新壁山中学体育馆的照明工程由甲、乙两对合作12天可以完成,共需工程费用138000元,乙队单独完成这些工程所需时间是甲队单独完成这项工程所需时间的2倍,且甲队每天工程费用要比乙队每天的工程费用多4500元.
(1)甲、乙两队单独完成这项工程分别需要多少天?
(2)若工程管理部门最初决定从这两个队中选一个队单独完成这项工程,从节约资金的角度考虑,应该选择哪个工程队?请说明理由.
(3)在招标过程中,工程管理部门接到县政府的通知,该工程必须在30天内(包括30天)完成,且工程费用不得超过132000元,为了按照县政府的要求完成该项工程,请问安排两个工程队施工时间(每个队的施工时间均为整数天)的方案有几种?哪种方案最节约工程费用?最省的工程费用是多少?
(1)甲、乙两队单独完成这项工程分别需要多少天?
(2)若工程管理部门最初决定从这两个队中选一个队单独完成这项工程,从节约资金的角度考虑,应该选择哪个工程队?请说明理由.
(3)在招标过程中,工程管理部门接到县政府的通知,该工程必须在30天内(包括30天)完成,且工程费用不得超过132000元,为了按照县政府的要求完成该项工程,请问安排两个工程队施工时间(每个队的施工时间均为整数天)的方案有几种?哪种方案最节约工程费用?最省的工程费用是多少?
考点:分式方程的应用,一元一次方程的应用,一元一次不等式的应用
专题:
分析:(1)求的是工效,工作时间较明显,一定是根据工作总量来列等量关系,本题的关键描述语是:甲、乙两队合作,则12天可以完成.等量关系为:甲12天的工作量+乙12天的工作量=1;
(2)设出乙队每天的工程费用为a元,则甲队每天的工程费用为a+4500元,列出方程求得各自独干的费用,分别计算工作总费用,进一步比较得出结论即可;
(3)先设甲施工a天,乙b天,根据使该工程施工总费用不超过132000元,列出方程和不等式组,求出答案即可.
(2)设出乙队每天的工程费用为a元,则甲队每天的工程费用为a+4500元,列出方程求得各自独干的费用,分别计算工作总费用,进一步比较得出结论即可;
(3)先设甲施工a天,乙b天,根据使该工程施工总费用不超过132000元,列出方程和不等式组,求出答案即可.
解答:解:(1)设甲队单独完成这项工程所需时间为x天,则乙队单独完成此项工程需2x天,
由题意得:
+
=
解得:x=18
经检验:x=18是原方程的解
2x=36
答:甲队单独完成这项工程需要18天,乙队单独完成此项工程需要36天.
(2)乙队每天的工程费用为a元,则甲队每天的工程费用为a+4500元,由题意得
12a+12(a+4500)=138000
解得:a=3500,
则a+4500=8000元,
如果工程由甲队单独完成,需要费用:8000×18=144000(元)
如果工程由乙队单独完成,需要费用:3500×36=126000(元)
126000<144000
答:工程应由乙队单独完成.
(3)设甲至多施工a天,乙b天,由题意得
+
=1
解得:b=36-2a;
解得:6≤a≤6,
即a=6,
则b=24.
所以方案有1种,即甲施工6天,乙24天.
由题意得:
| 1 |
| x |
| 1 |
| 2x |
| 1 |
| 12 |
解得:x=18
经检验:x=18是原方程的解
2x=36
答:甲队单独完成这项工程需要18天,乙队单独完成此项工程需要36天.
(2)乙队每天的工程费用为a元,则甲队每天的工程费用为a+4500元,由题意得
12a+12(a+4500)=138000
解得:a=3500,
则a+4500=8000元,
如果工程由甲队单独完成,需要费用:8000×18=144000(元)
如果工程由乙队单独完成,需要费用:3500×36=126000(元)
126000<144000
答:工程应由乙队单独完成.
(3)设甲至多施工a天,乙b天,由题意得
| a |
| 18 |
| b |
| 36 |
解得:b=36-2a;
|
解得:6≤a≤6,
即a=6,
则b=24.
所以方案有1种,即甲施工6天,乙24天.
点评:本题考查分式方程、一元一次方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.注意多种情况进行分析.

练习册系列答案
相关题目
 如图,在半径为10的⊙O中,AB、CD是互相垂直的两条相等的弦,垂足为P,若OP=6
如图,在半径为10的⊙O中,AB、CD是互相垂直的两条相等的弦,垂足为P,若OP=6| 2 |
| A、12 | B、14 | C、16 | D、18 |
在△ABC中,∠A=∠B=45°,则△ABC是( )
| A、直角三角形 |
| B、锐角三角形 |
| C、钝角三角形 |
| D、以上都不是 |
 如图所示,长方形由大小不一的正方形组成,原来的长方形的周长为68cm,那么原来长方形的长为( )
如图所示,长方形由大小不一的正方形组成,原来的长方形的周长为68cm,那么原来长方形的长为( )| A、18cm | B、20cm |
| C、16cm | D、22cm |
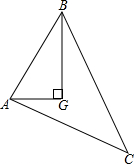 如图所示,点G是△ABC的重心,GA⊥GB,AB=5,则AC2+BC2的值为
如图所示,点G是△ABC的重心,GA⊥GB,AB=5,则AC2+BC2的值为 如图,∠AOB是直角,∠BOC=50°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为
如图,∠AOB是直角,∠BOC=50°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为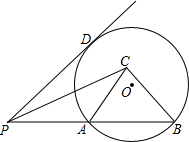 如图,PD切⊙O于D,PC=PD,B为⊙O上一点,PB交⊙O于A,连结AC、BC.求证:AC•PB=PC•BC.
如图,PD切⊙O于D,PC=PD,B为⊙O上一点,PB交⊙O于A,连结AC、BC.求证:AC•PB=PC•BC.