题目内容
5.如图,已知矩形纸片BDEF和直角三角板BCA,点A在EF上,AC=DE=$\sqrt{3}$,FE=3$\sqrt{5}$,∠C=90°,∠CBA=30°.(1)写出三种不同类型的结论.
(2)将直角三角板BCA绕点B旋转,在旋转过程中,
①求点A与点E的最短距离.
②若将直角三角板绕点B从①中位置开始顺时针旋转α度(0≤α<360),使∠BAE=90°,求α的度数.
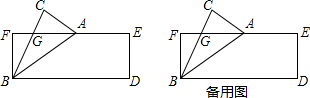
分析 (1)在RT△ABC中,由∠C=90°,∠ABC=30°,AC=$\sqrt{3}$可以求出∠BAC,AB,BC,通过AB=2BF得∠FAB=30°进而交于得到AG=BG.
(2)①如右图当A、B、E共线时,AE最小,求出BE即可.
②两种情形画出图形,求出∠EBA′和∠EBA″即可.
解答 解:(1)在RT△ABC中,∵∠C=90°,AC=$\sqrt{3}$,∠ABC=30°,
∴AB=2AC=2$\sqrt{3}$,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}$=3,∠BAC=90°-∠ABC=90°-60°=30°
∵四边形BDEF是矩形,
∴$BF=ED=AC=\sqrt{3}$,∠F=90°
∴AB=2BF,∠FAB=30°,
∴∠GBA=∠GAB,
∴GB=GA.
三个不同类型结论为:AB=2$\sqrt{3}$,∠BAC=60°,BG=GA.
(2)①如右图当A、B、E共线时,AE最小,连接BE,
∵四边形BDEF是矩形,
∴∠D=90°,BD=EF=3$\sqrt{5}$,BF=DE=$\sqrt{3}$,
∴BE=$\sqrt{B{D}^{2}+E{D}^{2}}$=$\sqrt{(3\sqrt{5})^{2}+(\sqrt{3})^{2}}$=4$\sqrt{3}$,
∴AE的最小值=BE-AB=4$\sqrt{3}$-2$\sqrt{3}$=2$\sqrt{3}$.
②在图1中,∵∠BA′E=90°,
∴cos∠EBA′=$\frac{A′B}{BE}$=$\frac{2\sqrt{3}}{4\sqrt{3}}$=$\frac{1}{2}$,
∴∠EBA′=60°同理在图2中,∠A″BE=60°,
∴旋转角α=60°或300°.
点评 本题考查直角三角形中30°的性质、勾股定理、三角函数的定义、旋转的性质等知识,利用三角函数值求角是解决最后一问的关键.

①5+4x=11;②3x-2x=1;③2x+y=5;④x2-5x+6=0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
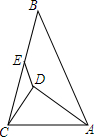 如图,△ABC中,AB=8cm,AC=5cm,AD平分∠BAC,且AD⊥CD,E为BC中点,则DE的长1.5cm.
如图,△ABC中,AB=8cm,AC=5cm,AD平分∠BAC,且AD⊥CD,E为BC中点,则DE的长1.5cm. 2015年年底,NBA运动员科比宣布将在本赛季结束后退役,一代名将即将告别喜欢他的无数球迷.如图是科比在一场比赛中正在投篮,已知该场比赛中,科比两分球和三分球一共投进了25个,两项共得57分.如果设他分别投中了x个两分球和y个三分球,可得二元一次方程组$\left\{\begin{array}{l}x+y=25\\ 2x+3y=57\end{array}\right.$.
2015年年底,NBA运动员科比宣布将在本赛季结束后退役,一代名将即将告别喜欢他的无数球迷.如图是科比在一场比赛中正在投篮,已知该场比赛中,科比两分球和三分球一共投进了25个,两项共得57分.如果设他分别投中了x个两分球和y个三分球,可得二元一次方程组$\left\{\begin{array}{l}x+y=25\\ 2x+3y=57\end{array}\right.$.