题目内容
10．解方程组：$\left\{\begin{array}{l}{m-\frac{n}{2}=2}\\{2m+3n=12}\end{array}\right.$．分析 方程组整理后，利用加减消元法求出解即可．
解答 解：方程组整理得：$\left\{\begin{array}{l}{2m-n=4①}\\{2m+3n=12②}\end{array}\right.$，
②-①得：4n=8，即n=2，
把n=2代入①得：m=3，
则方程组的解为$\left\{\begin{array}{l}{m=3}\\{n=2}\end{array}\right.$．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．运用平方差公式计算，错误的是（ ）
| A． | （a+b）（a-b）=a2-b2 | B． | （x+1）（x-1）=x2-1 | C． | （-a+b）（-a-b）=a2-b2 | D． | （2x+1）（2x-1）=2x2-1 |
1．下列四个数中，在-2到-1之间的数是（ ）
| A． | -1 | B． | $-\frac{1}{2}$ | C． | $-\frac{3}{2}$ | D． | 0 |
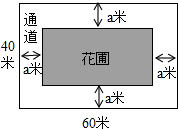如图，为美化校园环境，某校计划在一块长为60米，宽为40米的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修建成同样宽的通道，设通道宽为a米．
20．
如图，小手盖住的点的坐标可能为（ ）
如图，小手盖住的点的坐标可能为（ ）| A． | （4，3） | B． | （-4，3） | C． | （-4，-3） | D． | （4，-3） |