题目内容
15.(1)连续投掷一枚均匀的骰子三次,将掷得的点数一次作为百位、十位、个位数字组成一个三位数,求得到个位数字为5的三位数的概率.(2)如果将抛掷骰子换成摸球,即在不透明的袋中放入标有数字1,2,3,4,5,6的六个形状,大小完全相同的小球,依次从袋中摸出3个球(每次摸出一个球.且摸出的球不再放回袋中),将球上所标的数字分别作为百位、十位和个位数字组成-个三位数,那么得到个位数字为5的三位数的概率与(1)的结果相同吗?
分析 (1)利用概率的乘法公式得到共有216种等可能的结果数,可找出个位数字为5的三位数的结果数为36,然后根据概率公式计算;
(2)利用树状图可分析出共有120种等可能的结果数,再出个位数字为5的三位数的结果数为20,再计算出个位数字为5的三位数的概率,然后与(1)中的计算结果比较即可.
解答 解:(1)共有6×6×6=216种等可能的结果数,其中个位数字为5的三位数的结果数为6×6=36,
所以得到个位数字为5的三位数的概率=$\frac{36}{216}$=$\frac{1}{6}$;
(2)共有6×5×4=120种等可能的结果数,其中个位数字为5的三位数的结果数为5×4=20,
所以得到个位数字为5的三位数的概率=$\frac{20}{120}$=$\frac{1}{6}$,
所以得到个位数字为5的三位数的概率与(1)的结果相同.
点评 本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.

练习册系列答案
相关题目
20. 如图,小手盖住的点的坐标可能为( )
如图,小手盖住的点的坐标可能为( )
 如图,小手盖住的点的坐标可能为( )
如图,小手盖住的点的坐标可能为( )| A. | (4,3) | B. | (-4,3) | C. | (-4,-3) | D. | (4,-3) |
 如图,AB∥CD,AD=CD,∠1=70°,则∠2的度数是40°.
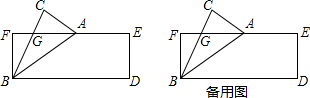
如图,AB∥CD,AD=CD,∠1=70°,则∠2的度数是40°. 在△ABC中,中线BD与高线CE交于F,EF=1,BE=2,△ABC的面积为20,则线段AE的长度为6.
在△ABC中,中线BD与高线CE交于F,EF=1,BE=2,△ABC的面积为20,则线段AE的长度为6.