题目内容
16.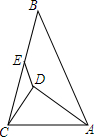 如图,△ABC中,AB=8cm,AC=5cm,AD平分∠BAC,且AD⊥CD,E为BC中点,则DE的长1.5cm.
如图,△ABC中,AB=8cm,AC=5cm,AD平分∠BAC,且AD⊥CD,E为BC中点,则DE的长1.5cm.
分析 延长CD交AB于F点.根据AD平分∠BAC,且AD⊥CD,证明△ACD≌△AFD,得D是CF的中点;又E为BC中点,所以DE是△BCF的中位线,利用中位线定理求解.
解答 解:延长CD交AB于F点.如图所示: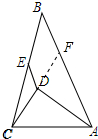
∵AD平分∠BAC,
∴∠FAD=∠CAD;
∵AD⊥CD,
∴∠ADF=∠ADC;
在△ACD和△AFD中,$\left\{\begin{array}{l}{∠ADF=∠ADC}&{\;}\\{AD=AD}&{\;}\\{∠FAD=CAD}&{\;}\end{array}\right.$,
∴△ACD≌△AFD(ASA),
∴CD=DF,AF=AC=5cm.
∵E为BC中点,BF=AB-AF=8-5=3,
∴DE=$\frac{1}{2}$BF=1.5(cm).
故答案为:1.5.
点评 此题考查了三角形中位线定理、等腰三角形的性质、全等三角形的判定与性质;通过作辅助线证明三角形全等得出CD=DF是解决问题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
6.已知圆锥的底面半径为3cm,母线长为4cm,则圆锥的全面积是( )
| A. | 15πcm2 | B. | 15cm2 | C. | 21πcm2 | D. | 24πcm2 |
1.下列四个数中,在-2到-1之间的数是( )
| A. | -1 | B. | $-\frac{1}{2}$ | C. | $-\frac{3}{2}$ | D. | 0 |
 如图,AB、CD、EF是与路灯在同一直线上的三个等高的标杆,相邻的两个标杆之间的距离都是2m,已知AB、CD在路灯光下的影长分别为BM=1.6m,DN=0.6m.求标杆EF的影长.
如图,AB、CD、EF是与路灯在同一直线上的三个等高的标杆,相邻的两个标杆之间的距离都是2m,已知AB、CD在路灯光下的影长分别为BM=1.6m,DN=0.6m.求标杆EF的影长.