题目内容
3.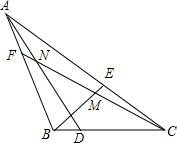 点D、E、F分别在△ABC的BC,CA,AB边上,∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,BE、CF交于点M,CF、AD交于点N,且满足∠BMF=2∠CND,那么∠BAC等于$\frac{180}{7}$(度).
点D、E、F分别在△ABC的BC,CA,AB边上,∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,BE、CF交于点M,CF、AD交于点N,且满足∠BMF=2∠CND,那么∠BAC等于$\frac{180}{7}$(度).
分析 由∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF易得各角与∠ABC、∠ACB、∠BAC之间的关系,由三角形外角等于不相邻的两个内角和表示出∠BMF与∠CND,再利用∠BMF=2∠CND可得出∠ABC+∠ACB=6∠BAC,再结合三角形内角和为180°可得出结论.
解答 解:∵∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,
∴∠CAD=$\frac{3}{4}$BAC,∠BAD=$\frac{1}{4}$∠BAC,∠ABE=$\frac{3}{4}$∠ABC,∠EBC=$\frac{1}{4}$∠ABC,∠BCF=$\frac{3}{4}$∠ACB,∠ACF=$\frac{1}{4}$∠ACB.
∠BMF=∠EBC+∠BCF=$\frac{1}{4}$∠ABC+$\frac{3}{4}$∠ACB;
∠CND=∠CAD+∠ACF=$\frac{3}{4}$∠BAC+$\frac{1}{4}$∠ACB;
∵∠BMF=2∠CND,即$\frac{1}{4}$∠ABC+$\frac{3}{4}$∠ACB=2×($\frac{3}{4}$∠BAC+$\frac{1}{4}$∠ACB),
∴∠ABC+∠ACB=6∠BAC,
又∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=$\frac{180°}{7}$.
故答案为:$\frac{180}{7}$.
点评 本题考查了三角形的内角和定理以及三角形的外角定理.解题的关键是由∠BMF=2∠CND找出∠ABC+∠ACB=6∠BAC.本题属于中档题,难度不大,但在角的变化上稍显繁琐,一不注意就易失分,做形如此类题型时,牢牢把握等量关系是关键.

练习册系列答案
相关题目
16.已知a+b=50,则a3+150ab+b3的值是( )
| A. | 125000 | B. | 125001 | C. | 125005 | D. | 125050 |
17.关于x的方程x2-mx+2=0的两根和是3,两根积是2,则m的值是( )
| A. | -3 | B. | 3 | C. | 2 | D. | -2 |
8.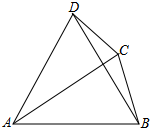 如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
 如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )| A. | 18° | B. | 20° | C. | 25° | D. | 15° |
15. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )| A. | 8 | B. | 10 | C. | 2$\sqrt{21}$或8 | D. | 2$\sqrt{21}$或10 |
12.一个三角形的两边长为4和6,第三边的边长是方程(x-2)(x-5)=0的根,则这个三角形的周长为( )
| A. | 12 | B. | 15 | C. | 12或15 | D. | 以上都不对 |
13.在平面直角坐标系中,若点M的坐标是(m,n),且点M在第二象限,则mn的值( )
| A. | <0 | B. | >0 | C. | =0 | D. | 不能确定 |
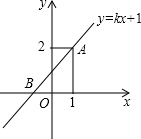 如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$).
如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$).