Question

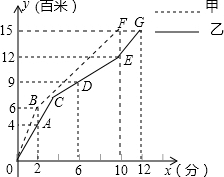甲、乙两人在200米的环形跑道上进行1500米赛跑，乙出发x₁分钟第一次改速，两人所跑路程y（百米）与时间x（分钟）之间的关系如图．请结合图象回答下列问题：
（1）请直接写出x₁=

 

分钟．
（2）若乙出发8分钟后提高速度并匀速跑至终点，结果和甲同时到达，乙的速度应是多少？
（3）请直接写出在0≤x≤10的范围内甲比乙多跑50米的时间．

Answer 1

考点：一次函数的应用

专题：

分析：（1）首先设CO的解析式为y=kx，再代入A点坐标可得CO的解析式．设CE的解析式为y=ax+b，再代入D（6，9），E（10，12），求出函数解析式，联立两个函数解析式求出C点坐标；
（2）利用路程除以时间可得速度；
（3）根据图象可得甲比乙多跑50米时，时间在2分钟内，求出OB解析式，再根据路程关系利用两个函数解析式列出方程．

解答：解：（1）设CO的解析式为y=kx，
∵A（2，4），
∴4=2k，
解得：k=2，
∴CO的解析式为y=2x，
设CE的解析式为y=ax+b，
∵D（6，9），E（10，12），
∴

9=6a+b 12=10a+b

，
解得：

a= 3 4 b= 9 2

，
∴y=

3

4

x+

9

2

，
联立两个函数解析式

y=2x y= 3 4 x+ 9 2

，
解得：

x= 18 5 y= 36 5

，
∴C（

18

5

，

36

5

），
∴x₁=

18

5

；
故答案为：

18

5

．

（2）当x=8时，y=

3

4

×8+

9

2

=10.5，
（15-10.5）÷（10-8）=2.25百米/分=225米/分；

（3）根据图象可得甲比乙多跑50米时，时间在2分钟内，
设BO的解析式为y=mx，
∵B（2，6），
∴6=2m，
解得：m=3，
∴y=3x，
由题意得：3x-2x=0.5，
解得：x=

1

2

．

点评：此题主要考查了一次函数解析式应用，关键是正确掌握待定系数法求一次函数解析式．