题目内容
 如图,将矩形ABCD放置在直角坐标系内,已知A(3,3),AB=4,AD=3,若将矩形向左平移a个单位,在向下平移a个单位(a>0),得矩形EFGH.
如图,将矩形ABCD放置在直角坐标系内,已知A(3,3),AB=4,AD=3,若将矩形向左平移a个单位,在向下平移a个单位(a>0),得矩形EFGH.(1)求点C、F的坐标;
(2)若在平移过程中,矩形EFGH恰好有两个顶点落在某反比例函数的图象上,求相应的a的值.
考点:反比例函数综合题
专题:综合题
分析:(1)根据矩形的性质得BC=AD=3,由点A的坐标易得B(7,3),C(7,6),然后根据平移与坐标变换得到F点的坐标为(7-a,3-a);
(2)根据平移与坐标变换得到H点的坐标为(3-a,6-a),G点坐标为(7-a,6-a),E点坐标为(3-a,3-a),由于在平移过程中,矩形EFGH恰好有两个顶点落在某反比例函数的图象上,则只有H点和F点或G点与E点,当点H和点F在某反比例函数的图象上,根据反比例函数图象上点的坐标特征得(3-a)•(6-a)=(7-a)•(3-a),解得a=3,不合题意舍去;当点G和点E在某反比例函数的图象上,根据反比例函数图象上点的坐标特征得(7-a)•(6-a)=(3-a)•(3-a),解得a=
.
(2)根据平移与坐标变换得到H点的坐标为(3-a,6-a),G点坐标为(7-a,6-a),E点坐标为(3-a,3-a),由于在平移过程中,矩形EFGH恰好有两个顶点落在某反比例函数的图象上,则只有H点和F点或G点与E点,当点H和点F在某反比例函数的图象上,根据反比例函数图象上点的坐标特征得(3-a)•(6-a)=(7-a)•(3-a),解得a=3,不合题意舍去;当点G和点E在某反比例函数的图象上,根据反比例函数图象上点的坐标特征得(7-a)•(6-a)=(3-a)•(3-a),解得a=
| 33 |
| 7 |
解答: 解:(1)∵四边形ABCD为矩形,
解:(1)∵四边形ABCD为矩形,
∴BC=AD=3,
∵A(3,3),AB=4,
∴B点坐标为(7,3),
∴C点坐标为(7,6),
∵将矩形向左平移a个单位,在向下平移a个单位(a>0),得矩形EFGH,
∴F点的坐标为(7-a,3-a);
(2)∵A(3,3),AD=3,
∴D点坐标为(3,6),
∵将矩形向左平移a个单位,在向下平移a个单位(a>0),得矩形EFGH,
∴H点的坐标为(3-a,6-a),G点坐标为(7-a,6-a),E点坐标为(3-a,3-a),
当点H和点F在某反比例函数的图象上,则(3-a)•(6-a)=(7-a)•(3-a),解得a=3,此时H、F点在坐标轴上,不合题意舍去;
当点G和点E在某反比例函数的图象上,则(7-a)•(6-a)=(3-a)•(3-a),解得a=
,
∴a的值为
.
 解:(1)∵四边形ABCD为矩形,
解:(1)∵四边形ABCD为矩形,∴BC=AD=3,
∵A(3,3),AB=4,
∴B点坐标为(7,3),
∴C点坐标为(7,6),
∵将矩形向左平移a个单位,在向下平移a个单位(a>0),得矩形EFGH,
∴F点的坐标为(7-a,3-a);
(2)∵A(3,3),AD=3,
∴D点坐标为(3,6),
∵将矩形向左平移a个单位,在向下平移a个单位(a>0),得矩形EFGH,
∴H点的坐标为(3-a,6-a),G点坐标为(7-a,6-a),E点坐标为(3-a,3-a),
当点H和点F在某反比例函数的图象上,则(3-a)•(6-a)=(7-a)•(3-a),解得a=3,此时H、F点在坐标轴上,不合题意舍去;
当点G和点E在某反比例函数的图象上,则(7-a)•(6-a)=(3-a)•(3-a),解得a=
| 33 |
| 7 |
∴a的值为
| 33 |
| 7 |
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和矩形的性质;了解平移与坐标变换.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列图案中,既不是中心对称图形也不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |

 如图,一次函数y=kx+b与反比例函数y=
如图,一次函数y=kx+b与反比例函数y= 某市对火车站进行了大规模的改建,改建后的火车站除原有的普通售票窗口外,新增了自动打印车票的无人售票窗口.如图,线段OA和OB分别表示某日从上午8点到上午11点,每个普通售票窗口售出的车票数w1(张)和每个无人售票窗口售出的车票数w2(张)关于售票时间t(小时)的函数图象.
某市对火车站进行了大规模的改建,改建后的火车站除原有的普通售票窗口外,新增了自动打印车票的无人售票窗口.如图,线段OA和OB分别表示某日从上午8点到上午11点,每个普通售票窗口售出的车票数w1(张)和每个无人售票窗口售出的车票数w2(张)关于售票时间t(小时)的函数图象.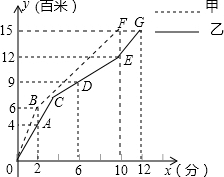 甲、乙两人在200米的环形跑道上进行1500米赛跑,乙出发x1分钟第一次改速,两人所跑路程y(百米)与时间x(分钟)之间的关系如图.请结合图象回答下列问题:
甲、乙两人在200米的环形跑道上进行1500米赛跑,乙出发x1分钟第一次改速,两人所跑路程y(百米)与时间x(分钟)之间的关系如图.请结合图象回答下列问题: 如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为
如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为