题目内容
 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为考点:二次函数综合题
专题:
分析:连接AC,BC,有抛物线的解析式可求出A,B,C的坐标,进而求出AO,BO,DO的长,在直角三角形ACB中,利用射影定理可求出CO的长,进而可求出CD的长.
解答: 解:连接AC,BC,
解:连接AC,BC,
∵抛物线的解析式为y=x2-2x-3,
∴点D的坐标为(0,-3),
∴OD的长为3,
设y=0,则0=x2-2x-3,
解得:x=-1或3,
∴A(-1,0),B(3,0)
∴AO=1,BO=3,
∵AB为半圆的直径,
∴∠ACB=90°,
∵CO⊥AB,
∴CO2=AO•BO=3,
∴CO=
,
∴CD=CO+OD=3+
,
故答案为:3+
.
 解:连接AC,BC,
解:连接AC,BC,∵抛物线的解析式为y=x2-2x-3,
∴点D的坐标为(0,-3),
∴OD的长为3,
设y=0,则0=x2-2x-3,
解得:x=-1或3,
∴A(-1,0),B(3,0)
∴AO=1,BO=3,
∵AB为半圆的直径,
∴∠ACB=90°,
∵CO⊥AB,
∴CO2=AO•BO=3,
∴CO=
| 3 |
∴CD=CO+OD=3+
| 3 |
故答案为:3+
| 3 |
点评:本题是二次函数综合题型,主要考查了抛物线与坐标轴的交点问题、解一元二次方程、圆周角定理、射影定理,读懂题目信息,理解“果圆”的定义是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,∠ABC=40°,以AB为直径作圆交BC于点D,交CA的延长线于点E,若点E在BD的垂直平分线上,则∠C的度数为( )
如图,在△ABC中,∠ABC=40°,以AB为直径作圆交BC于点D,交CA的延长线于点E,若点E在BD的垂直平分线上,则∠C的度数为( )| A、25° | B、30° |
| C、35° | D、40° |
 如图,一次函数y=kx+b与反比例函数y=
如图,一次函数y=kx+b与反比例函数y= 甲、乙两人在200米的环形跑道上进行1500米赛跑,乙出发x1分钟第一次改速,两人所跑路程y(百米)与时间x(分钟)之间的关系如图.请结合图象回答下列问题:
甲、乙两人在200米的环形跑道上进行1500米赛跑,乙出发x1分钟第一次改速,两人所跑路程y(百米)与时间x(分钟)之间的关系如图.请结合图象回答下列问题: 已知直线l:y=-
已知直线l:y=- 如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为
如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为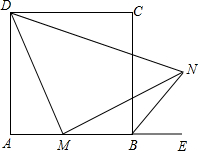 正方形ABCD中,M是AB上的一点,E是AB的延长线上一点,N是∠CBE的平分线上一点,且MN=DM.
正方形ABCD中,M是AB上的一点,E是AB的延长线上一点,N是∠CBE的平分线上一点,且MN=DM. (1)计算:(2013-π)0+4sin60°-
(1)计算:(2013-π)0+4sin60°-