题目内容
在△ABC中,点I是内心,若∠A=40°,则∠BIC的度数为 .
考点:三角形的内切圆与内心
专题:
分析:根据三角形内角和定理即可求得∠IBC+∠ICB的度数,然后根据内心的定义即可求得∠IBC+∠ICB,然后根据三角形内角和定理即可求解.
解答: 解:∵∠A=40°,
解:∵∠A=40°,
∴∠ABC+∠ACB=180°-40°=140°.
∵点I是△ABC的内心,
∴∠IBC=
∠ABC,∠ICB=
∠ACB,
∴∠IBC+∠ICB=
(∠ABC+∠ACB)=70°,
∴∠BIC=180°-(∠IBC+∠ICB)=110°.
故答案是:110°.
 解:∵∠A=40°,
解:∵∠A=40°,∴∠ABC+∠ACB=180°-40°=140°.
∵点I是△ABC的内心,
∴∠IBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠IBC+∠ICB=
| 1 |
| 2 |
∴∠BIC=180°-(∠IBC+∠ICB)=110°.
故答案是:110°.
点评:此题主要考查了三角形的内心的计算,正确理解∠IBC+∠ICB=
(∠ABC+∠ACB)是关键.
| 1 |
| 2 |

练习册系列答案
相关题目
由四舍五入法得到的近似数8.02×104,下列说法正确的是( )
| A、精确到十分位,有3个有效数字 |
| B、精确到个位,有2个有效数字 |
| C、精确到百位,有3个有效数字 |
| D、精确到千位,有4个有效数字 |

 某市对火车站进行了大规模的改建,改建后的火车站除原有的普通售票窗口外,新增了自动打印车票的无人售票窗口.如图,线段OA和OB分别表示某日从上午8点到上午11点,每个普通售票窗口售出的车票数w1(张)和每个无人售票窗口售出的车票数w2(张)关于售票时间t(小时)的函数图象.
某市对火车站进行了大规模的改建,改建后的火车站除原有的普通售票窗口外,新增了自动打印车票的无人售票窗口.如图,线段OA和OB分别表示某日从上午8点到上午11点,每个普通售票窗口售出的车票数w1(张)和每个无人售票窗口售出的车票数w2(张)关于售票时间t(小时)的函数图象.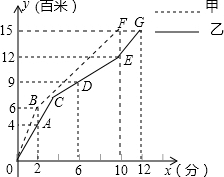 甲、乙两人在200米的环形跑道上进行1500米赛跑,乙出发x1分钟第一次改速,两人所跑路程y(百米)与时间x(分钟)之间的关系如图.请结合图象回答下列问题:
甲、乙两人在200米的环形跑道上进行1500米赛跑,乙出发x1分钟第一次改速,两人所跑路程y(百米)与时间x(分钟)之间的关系如图.请结合图象回答下列问题: 一个有进水管与出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的若干分内既进水又出水,之后只出水不进水.每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图.则a=
一个有进水管与出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的若干分内既进水又出水,之后只出水不进水.每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图.则a= 如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为
如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为