题目内容
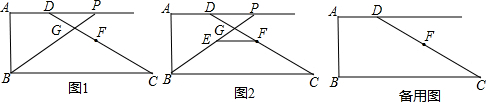
 如图,已知菱形ABCD的边长为2,∠B=60°,点P、Q分别是边BC、CD上的动点(不与端点重合),且BP=CQ.
如图,已知菱形ABCD的边长为2,∠B=60°,点P、Q分别是边BC、CD上的动点(不与端点重合),且BP=CQ.(1)图中除了△ABC与△ADC外,还有哪些三角形全等,请写出来;
(2)点P、Q在运动过程中,四边形APCQ的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
(3)当点P在什么位置时,△PCQ的面积最大,并请说明理由.
考点:菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)△ABP≌△ACQ,△APC≌△AQD,根据等边三角形的性质以及菱形的性质证明即可;
(2)面积不变,根据三角形ACP和三角形ADQ全等,则四边形APCQ的面积等于三角形ABC或者三角形ACD的面积.
(3)要使三角形PCQ的面积最大,只要等边三角形APQ的面积最小即AP⊥BC时即可.
(2)面积不变,根据三角形ACP和三角形ADQ全等,则四边形APCQ的面积等于三角形ABC或者三角形ACD的面积.
(3)要使三角形PCQ的面积最大,只要等边三角形APQ的面积最小即AP⊥BC时即可.
解答:解:(1)△ABP≌△ACQ,△APC≌△AQD,
在菱形ABCD中,∵∠B=60°,∴△ABC是等边三角形,
∴AB=BC=AC,
∴AC=CD,
∵∠PAQ=60°,
∴∠CAP=∠DAQ,
∴△ACP≌△ADQ,
同理:△ABP≌△ACQ;
(2)四边形的面积不变为定值,
理由如下:
∵△ACP≌△ADQ,∴S△ACP=S△ADQ,
即S四边形APCQ=S△ACD=
×2×
=
;
(3)∵△PAQ是等边三角形,
∴当AP⊥BC时,三角形APQ的面积最小,则三角形PCQ的面积最大.
此时BP=1,即点P在点B右边距离为1时,三角形PCQ的面积最大.
在菱形ABCD中,∵∠B=60°,∴△ABC是等边三角形,
∴AB=BC=AC,
∴AC=CD,
∵∠PAQ=60°,
∴∠CAP=∠DAQ,
∴△ACP≌△ADQ,
同理:△ABP≌△ACQ;
(2)四边形的面积不变为定值,
理由如下:
∵△ACP≌△ADQ,∴S△ACP=S△ADQ,
即S四边形APCQ=S△ACD=
| 1 |
| 2 |
| 3 |
| 3 |
(3)∵△PAQ是等边三角形,
∴当AP⊥BC时,三角形APQ的面积最小,则三角形PCQ的面积最大.
此时BP=1,即点P在点B右边距离为1时,三角形PCQ的面积最大.
点评:本题考查了菱形的性质、全等三角形的判定和性质以及等边三角形的判定,有一个角等于60度的等腰三角形是等边三角形.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
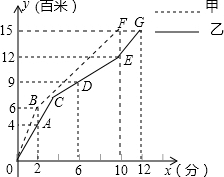 甲、乙两人在200米的环形跑道上进行1500米赛跑,乙出发x1分钟第一次改速,两人所跑路程y(百米)与时间x(分钟)之间的关系如图.请结合图象回答下列问题:
甲、乙两人在200米的环形跑道上进行1500米赛跑,乙出发x1分钟第一次改速,两人所跑路程y(百米)与时间x(分钟)之间的关系如图.请结合图象回答下列问题: 如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为
如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为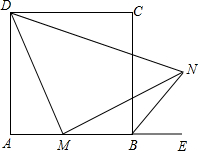 正方形ABCD中,M是AB上的一点,E是AB的延长线上一点,N是∠CBE的平分线上一点,且MN=DM.
正方形ABCD中,M是AB上的一点,E是AB的延长线上一点,N是∠CBE的平分线上一点,且MN=DM.