题目内容
 如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.
如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.(1)求证:∠PAC=∠B;
(2)若BC=6,⊙O半径为5,求PA的长.
考点:切线的性质,勾股定理,相似三角形的判定与性质
专题:计算题
分析:(1)由PA为圆O的切线,且AB为直角,利用切线的性质及直角所对的圆周角为直角,得到两个角为直角,利用同角的余角相等即可得证;
(2)在直角三角形ABC中,根据勾股定理求出AC的长,根据(1)的结论,再由一对直角相等,得到三角形PAD与三角形ABC相似,由相似得比例根据AB,AD以及BC的长,即可确定出PA的长.
(2)在直角三角形ABC中,根据勾股定理求出AC的长,根据(1)的结论,再由一对直角相等,得到三角形PAD与三角形ABC相似,由相似得比例根据AB,AD以及BC的长,即可确定出PA的长.
解答:(1)证明:∵PA为圆O的切线,且AB为直径,
∴∠PAO=90°,∠C=90°,
∴∠PAC+∠BAC=90°,∠B+∠BAC=90°,
∴∠PAC=∠B;
(2)解:在Rt△ACB中,根据勾股定理得:AC=
=8,
由(1)得:∠PAC=∠B,
∵OP⊥AC,∴∠ADP=∠C=90°,
∴△PAD∽△ABC,
∴PA:AB=AD:BC,
∵AC⊥OD,
∴AD=CD=4,
∴PA=
=
=
.
∴∠PAO=90°,∠C=90°,
∴∠PAC+∠BAC=90°,∠B+∠BAC=90°,
∴∠PAC=∠B;
(2)解:在Rt△ACB中,根据勾股定理得:AC=
| AB2-BC2 |
由(1)得:∠PAC=∠B,
∵OP⊥AC,∴∠ADP=∠C=90°,
∴△PAD∽△ABC,
∴PA:AB=AD:BC,
∵AC⊥OD,
∴AD=CD=4,
∴PA=
| AB•AD |
| BC |
| 10×4 |
| 6 |
| 20 |
| 3 |
点评:此题考查了切线的性质,圆周角定理,勾股定理,以及相似三角形的判定与性质,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
4的相反数是( )
| A、±2 | ||
| B、-4 | ||
| C、2 | ||
D、
|
 如图,过双曲线y=
如图,过双曲线y= 如图,一次函数y=kx+b与反比例函数y=
如图,一次函数y=kx+b与反比例函数y= 如图,矩形ABCD中,AB=3,AD=5,点E在AD上,且AE:ED=1:4,联结BE,射线EF⊥BE交边DC于点F.求CF的长.
如图,矩形ABCD中,AB=3,AD=5,点E在AD上,且AE:ED=1:4,联结BE,射线EF⊥BE交边DC于点F.求CF的长.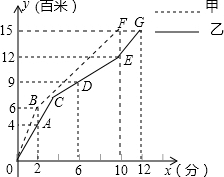 甲、乙两人在200米的环形跑道上进行1500米赛跑,乙出发x1分钟第一次改速,两人所跑路程y(百米)与时间x(分钟)之间的关系如图.请结合图象回答下列问题:
甲、乙两人在200米的环形跑道上进行1500米赛跑,乙出发x1分钟第一次改速,两人所跑路程y(百米)与时间x(分钟)之间的关系如图.请结合图象回答下列问题: 已知直线l:y=-
已知直线l:y=- 如图,在菱形ABCD中,AB=2,∠B=60°.将一个60°的∠PCQ的顶点放在点C处,并绕点C旋转,当CP与AB交于点M,CQ同时与AD交于点N时.
如图,在菱形ABCD中,AB=2,∠B=60°.将一个60°的∠PCQ的顶点放在点C处,并绕点C旋转,当CP与AB交于点M,CQ同时与AD交于点N时.