题目内容
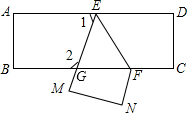把一长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D、C分别在M、N的位置上，若∠EFG=50°，则∠1的度数是（ ）| A、90° | B、80° |
| C、70° | D、60° |
考点：平行线的性质,翻折变换（折叠问题）
专题：计算题
分析：先根据矩形的性质得AD∥BC，再根据平行线的性质得∠DEF=∠EFG=50°，接着根据折叠的性质得到∠DEF=∠MEF=50°，然后利用平角的定义，利用∠1=180°-∠DEF-∠MEF进行计算即可．
解答：
解：∵四边形ABCD为矩形，
∴AD∥BC，
∴∠DEF=∠EFG=50°，
∵长方形纸片ABCD沿EF折叠后ED与BC的交点为G，
∴∠DEF=∠MEF=50°，
∴∠1=180°-∠DEF-∠MEF=80°．
故选B．
∴AD∥BC，
∴∠DEF=∠EFG=50°，
∵长方形纸片ABCD沿EF折叠后ED与BC的交点为G，
∴∠DEF=∠MEF=50°，
∴∠1=180°-∠DEF-∠MEF=80°．
故选B．
点评：本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．也考查了折叠的性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
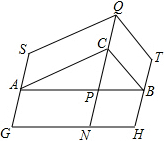如图，△ABC中，∠ACB=90°，分别以它的三边向外作平行四边形，QC∥GS∥TH交AB于P，交GH于N，且QC=PN，若?ABHG和?SQCA的面积分别为8和6，则?QTBC的面积为
一个几何体的三视图如图所示，根据图示的数据计算出该几何体的表面积．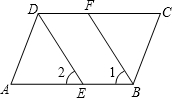
已知：BF，DE分别平分∠ABC和∠ADC，∠1=∠2，∠ADC=∠ABC，由此可推得图中哪些线段平行？并写出你的推理过程．
如图，已知AB∥CD，CE交AB于F，若∠1=50°，则∠C的度数为（ ）| A、40° | B、50° |
| C、60° | D、130° |
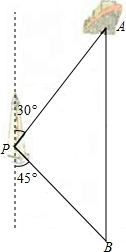如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为