题目内容
 一个几何体的三视图如图所示,根据图示的数据计算出该几何体的表面积.
一个几何体的三视图如图所示,根据图示的数据计算出该几何体的表面积.考点:圆锥的计算,由三视图判断几何体
专题:计算题
分析:根据三视图可判断该几何体是圆锥,圆锥的高为12,圆锥的底面圆的半径为5,再利用勾股定理计算出母线长,然后求底面积与侧面积的和即可.
解答:
解:由三视图可知该几何体是圆锥,圆锥的高为12,圆锥的底面圆的半径为5,
所以圆锥的母线长=
=13,
所以圆锥的表面积=π•52+
•2π•5•13=90π.
所以圆锥的母线长=
| 52+122 |
所以圆锥的表面积=π•52+
| 1 |
| 2 |
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了三视图.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列图形中,∠1与∠2是对顶角的是( )
A、 |
B、 |
C、 |
D、 |
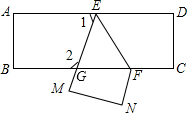 把一长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=50°,则∠1的度数是( )
把一长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=50°,则∠1的度数是( )| A、90° | B、80° |
| C、70° | D、60° |
 如图所示,将长方形ABCD沿EF折叠,使点B落在点G,点C落在点H处,若∠EFD=80°,求∠DFH的度数.
如图所示,将长方形ABCD沿EF折叠,使点B落在点G,点C落在点H处,若∠EFD=80°,求∠DFH的度数.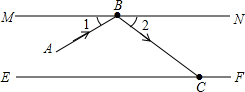 如图,MN,EF是两个互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:
如图,MN,EF是两个互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律: 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西n°,问:甲巡逻艇的航向?
如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西n°,问:甲巡逻艇的航向?