题目内容
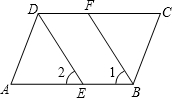 已知:BF,DE分别平分∠ABC和∠ADC,∠1=∠2,∠ADC=∠ABC,由此可推得图中哪些线段平行?并写出你的推理过程.
已知:BF,DE分别平分∠ABC和∠ADC,∠1=∠2,∠ADC=∠ABC,由此可推得图中哪些线段平行?并写出你的推理过程.考点:平行线的判定
专题:
分析:由∠1=∠2,可得DE∥BF;根据角平分线的性质可得∠FDE=
∠ADC,∠2=
∠ABC,再由∠ADC=∠ABC可得∠FDE=∠2,进而可推出∠1=∠FDE,再根据内错角相等,两直线平行可得AB∥CD;进而可得:DF∥BE;由AB∥CD,可得∠ADC+∠A=180°,又因为∠ADC=∠ABC,所以可得:∠ABC+∠A=180°,然后根据同旁内角互补,两直线平行,即可判断AD∥BC.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:由题意可得:①DE∥BF;②AB∥CD;③DF∥BE;④AD∥BC.
理由:①∵∠1=∠2,
∴DE∥BF;
②∵DE,BF分别平分∠ADC和∠ABC,
∴∠FDE=
∠ADC,∠2=
∠ABC,
∵∠ADC=∠ABC,
∴∠FDE=∠2,
∵∠1=∠2,
∴∠1=∠FDE,
∴AB∥CD;
③∵DF在CD上,BE在AB上,且AB∥CD,
∴DF∥BE;
④∵AB∥CD,
∴∠ADC+∠A=180°,
∵∠ADC=∠ABC,
∴∠ABC+∠A=180°,
∴AD∥BC.
理由:①∵∠1=∠2,
∴DE∥BF;
②∵DE,BF分别平分∠ADC和∠ABC,
∴∠FDE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ADC=∠ABC,
∴∠FDE=∠2,
∵∠1=∠2,
∴∠1=∠FDE,
∴AB∥CD;
③∵DF在CD上,BE在AB上,且AB∥CD,
∴DF∥BE;
④∵AB∥CD,
∴∠ADC+∠A=180°,
∵∠ADC=∠ABC,
∴∠ABC+∠A=180°,
∴AD∥BC.
点评:此题考查了平行线的判定,利用角判断两直线平行的方法有:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
相关题目
如果函数y=(k-3)xk2-3k+2+kx+1是关于x的二次函数,那么k的值是( )
| A、1或2 | B、0或3 | C、3 | D、0 |
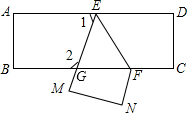 把一长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=50°,则∠1的度数是( )
把一长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=50°,则∠1的度数是( )| A、90° | B、80° |
| C、70° | D、60° |
 我国体育健儿在24届-30届奥运会上获得金牌的情况如图所示,则在这七届奥运会上,我国体育健儿共获得
我国体育健儿在24届-30届奥运会上获得金牌的情况如图所示,则在这七届奥运会上,我国体育健儿共获得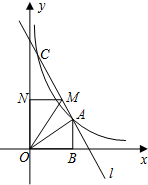 已知:如图,点A(2,m)在双曲线y=
已知:如图,点A(2,m)在双曲线y= 下图是画在方格纸上的某岛简图.
下图是画在方格纸上的某岛简图. 如图,做一个试管架,在长a cm的木条上钻4个圆孔,每个孔的半径均为2cm,则图中x为
如图,做一个试管架,在长a cm的木条上钻4个圆孔,每个孔的半径均为2cm,则图中x为